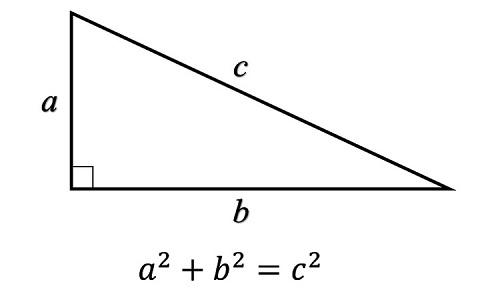
تابع در مشتقپذیر است هرگاه در این نقطه پیوسته باشد و مشتق چپ و راست تابع با هم برابر و مساوی یک عدد حقیقی معین باشد.
تعبیر هندسی مشتقپذیری: تابع در مشتقپذیر است هرگاه بتوان در این نقطه یک خط کامل مماس و غیر موازی با محور yها بر منحنی رسم کرد.
اگر تابع در نقطهٔ مشتقپذیر باشد، آنگاه در آن نقطه پیوسته نیز هست.
ولی عکس قضیهٔ فوق صحیح نمیباشد یعنی ممکن است تابع پیوسته باشد اما مشتقپذیر نباشد؛ به عبارت دیگر، پیوستگی تابع در شرط لازم برای مشتقپذیری تابع است، نه شرط کافی. پس اگر تابع در ناپیوسته باشد، آنگاه در مشتقپذیر نیست.
مواردی که تابع در نقطهٔ مفروض مشتقپذیر نیست:
منظور از دامنهٔ تابع مشتق مجموعهٔ نقاطی است که تابع در آنها مشتقپذیر است. بهطور کلی برای تابع داریم:
هرگاه بخواهیم مشتق یک تابع مانند را نسبت به تابع دیگری مانند بدست آوریم، کافی است مشتق این توابع را نسبت به متغیرشان محاسبه نموده و سپس برهم تقسیم کنیم.
توابع که به فرم هستند را توابع پارامتری مینامند. در این حالت، مشتق نسبت به از رابطهٔ زیر قابل محاسبه است:
به بیان دیگر، هرگاه تابعی از و تابعی از باشد، برای بدست آوردن مشتق نسبت به ، مشتق نسبت به را در مشتق نسبت به ضرب میکنیم.
همچنین به شکل دیگری برای توابع ، و داریم:

دو ریاضیدان در تاریخ ۷ سپتامبر اثبات خود برای مدلی از مشهورترین مسائل ریاضی را ارائه دادند. نتایج این اثبات، چشمانداز جدیدی به بررسی فرضیهی اعداد اول دوقلو باز کرده است که بیش از یک قرن ذهن ریاضیدانها را به خود مشغول کرده است. این فرضیه راهگشای پیچیدهترین مسائل علم حساب خواهد بود. بهگفتهی جیمز ماینارد، ریاضیدان دانشگاه آکسفورد:
- مدتها در حال درجا زدن بودیم و ایدهای برای حل این مسئله نداشتیم بنابراین وقتی ایدههای جدید مطرح شدند ناخودآگاه هیجانزده شدیم.
اعداد اول دوقلو، به زوج اعداد اول با تفاضل ۲ گفته میشود. زوجهای عددی ۵ و ۷ یا ۱۷ و ۱۹ از اعداد اول دوقلو هستند. براساس این فرضیه بینهایت زوج عدد اول دوقلو در میان اعداد صحیح وجود دارد. ریاضیدانها در زمینهی حل این فرضیه در دههی گذشته به شکل چشمگیری پیشرفت کردهاند اما تاکنون قادر به حل آن نشده بودند.
ویل ساوین از دانشگاه کلمبیا و مارک شوسترمان از دانشگاه ویسکانسین مادیسون در اثبات جدید خود، فرضیهی اعداد اول دوقلو را برای محدودهی کوچکتری از اعداد حل کردند. آنها این فرضیه را برای یک مجموعه از دستگاههای عددی متناهی ثابت کردند که ممکن است دربردارندهی مجموعهی محدودی از اعداد اول دوقلو باشد.

به دستگاههای عددی فوق، میدانهای متناهی» گفته میشود. با اینکه این مجموعه از نظر اندازه کوچک است اما میتوان اغلب ویژگیهای اعداد صحیح نامتناهی را در آن یافت. ریاضیدانها در تلاشاند به سؤالهای ریاضی روی میدانهای متناهی پاسخ دهند و نتایج را به اعداد صحیح هم تعمیم دهند. بهگفتهی ماینارد:
- برای رسیدن به رویایی نهایی در ابتدا باید به درک مناسبی از دنیای میدانهای متناهی رسید سپس این نتیجه میتواند راه خود را به دنیای اعداد صحیح باز کند.
ساوین و شوسترمان علاوه بر اثبات فرضیهی اعداد اول دوقلو به نتیجهی فراگیرتری دربارهی رفتار اعداد اول در دستگاههای عددی کوچک رسیدهاند. آنها به محاسبهی تعداد تکرار اعداد اول دوقلو روی بازههای کوچکتر پرداختند. از این نتیجه میتوان برای کنترل دقیقتر اعداد دوقلوی اول استفاده کرد. ریاضیدانها امیدوار هستند برای اعداد ترتیبی هم به نتایج مشابهی برسند؛ آنها اثبات جدید را برای اعداد اول روی محور حقیقی بررسی خواهند کرد.
براساس مشهورترین پیشبینی فرضیهی اعداد اول دوقلو میتوان بینهایت زوج عدد اول با تفاضل ۲ پیدا کرد؛ اما این فرضیه فراتر از صرفا تفاضل ۲ است. برای مثال میتوان بینهایت زوج عدد اول با اختلاف ۴ (مانند ۳ و ۷) یا ۱۴ (۲۹۳ و ۳۰۷) و بهطور کلی تفاضل دلخواه بیشتر از ۲ پیدا کرد.
آلفونس دی پولیگناک ، ریاضیدان فرانسوی، در سال ۱۸۴۹ از این فرضیه به شکل امروزی آن استفاده کرد. ریاضیدانها در طول ۱۶۰ سال پس از آلفونس پیشرفت کمی در اثبات این فرضیه داشتند؛ اما نهایتا در سال ۲۰۱۳ این سد شکسته شد. درهمان سال ییتانگ ژانگ ثابت کرد بینهایت زوج عدد اول با تفاضل حداکثر ۷۰ میلیون وجود دارد. سال بعد از این کشف ریاضیدانهای دیگری از جمله ماینارد و تری تائو شکاف اعداد اول را به شکل چشمگیری کاهش دادند. آخرین اثبات، وجود بینهایت زوج عدد اول با اختلاف حداکثر ۲۴۶ بود.
اما پیشرفت فرضیهی اعداد اول دوقلو متوقف شد. ریاضیدانها برای حل کامل این مسئله به ایدهای کاملا جدید نیاز دارند. دستگاههای عددی متناهی جای خوبی برای جستجوی این اعداد هستند. برای ساخت یک میدان متناهی باید به استخراج یک زیرمجموعهی عددی از اعداد طبیعی پرداخت. برای مثال در این روش پنج عدد انتخاب میشود (میتواند شامل اعداد اول هم باشد) و بهجای نمایش متداول اعداد روی محور حقیقی، روی صفحهی ساعت نمایش داده میشوند.
در مرحلهی بعدی محاسبات روی صفحهی ساعت انجام میشوند. برای مثال ۳+۴ در دستگاه عددی متناهی با پنج عدد چیست؟ از ۴ شروع کنید پس از طی سه فاصله اطراف ساعت به عدد ۲ میرسید. تفریق، ضرب و تقسیم هم عملکرد مشابهی دارند.
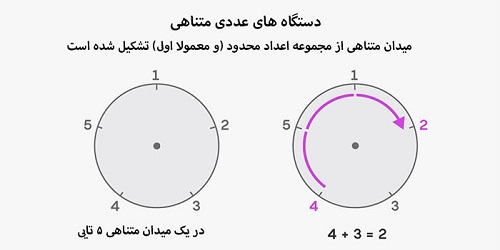
روش میدانهای متناهی تنها یک دستاورد دارد. مفهوم رایج اعداد اول در میدانهای متناهی شکل متفاوتی به خود میگیرد. در یک میدان متناهی هر عدد بر عدد دیگر بخشپذیر است. برای مثال، ۷ معمولا بر ۳ بخشپذیر نیست؛ اما در میدان متناهی با پنج عنصر، چنین رابطهای وجود دارد. به همین دلیل در این میدان متناهی، ۷ مشابه ۱۲ است هر دو در صفحهی ساعت روی ۲ قرار میگیرند؛ بنابراین ۷ تقسیم بر ۳ مشابه ۱۲ تقسیم بر ۳ است؛ و جواب ۱۲ تقسیم بر ۳ برابر با ۴ است.
به همین دلیل، فرضیهی اعداد دوقلوی اول برای میدانهای متناهی دربارهی چندجملهایهای اول مثل x۲+1 صدق میکند. برای مثال، فرض کنید میدان متناهی شما شامل اعداد ۱، ۲ و ۳ است. یک چندجملهای در این میدان متناهی اعدادی را بهعنوان ضریب دربردارد و چندجملهای اول، قابل تجزیه بر چندجملهایهای کوچکتر نیست؛ بنابراین x۲+x +۲ اول است زیرا نمیتوان آن را تجزیه کرد اما x۲-۱ اول نیست زیرا به (x+۱) و (x-۱) قابل تجزیه است.
در چندجملهایهای اول، یافتن چندجملهایهای اول دوقلو هم امری عادی است. چندجملهای اول دوقلو به یک زوج چندجملهای اطلاق میشود که هم اول باشند و هم اختلاف ثابتی با یکدیگر داشته باشند. برای مثال چندجملهای x۲+x +۲ مشابه x۲+۲x+۲ اول است. هر دو دارای اختلاف x هستند (برای رسیدن به چندجملهای دوم، x را به چندجملهای اول اضافه کنید). طبق فرضیهی اعداد اول دوقلو برای میدانهای متناهی، بینهایت زوج چندجملهای اول دوقلو وجود دارد که دارای اختلاف x یا اختلافهای دلخواه دیگر است.
شاید چندجملهایهای اول و میدانهای متناهی به نظر مصنوعی برسند و بهطور کلی کاربرد کمی در علم اعداد داشته باشند اما مشابه یک شبیهساز طوفان عمل میکنند؛ جهانی مستقل که از آن میتوان به دیدگاههایی دربارهی پدیدههای جهان واقعی رسید. بهگفتهی شوسترمان:
آندره وی در دههی ۱۹۴۰ روشی دقیق برای ترجمهی ریاضیات دستگاههای عددی کوچک به ریاضیات اعداد صحیح ابداع کرد؛ از همین نقطه میدانهای متناهی در مرکز توجه قرار گرفتند. او مهمترین مسئلهی ریاضی یعنی فرضیهی ریمان را برای منحنیهای روی میدانهای متناهی اثبات کرد (مسئلهای که بهعنوان فرضیهی ریمانی هندسی هم شناخته میشود). این اثبات همراهبا یک مجموعه از حدس و گمانهای وی، میدانهای متناهی را بهعنوان چشماندازی غنی برای اکتشافات ریاضی تبدیل کرده است.
براساس دیدگاه کلیدی آندره وی، در میدانهای متناهی میتوان از روشهای هندسی برای پاسخگویی به مسئلههای عددی استفاده کرد. شوسترمان میگوید: این ویژگی خاص میدانهای متناهی است که میتوان برای حل بسیاری از مسائل به بازتعریف هندسی آنها پرداخت.»
اعداد اول دوقلو به زوج اعداد اول با تفاضل مشخص گفته میشود.
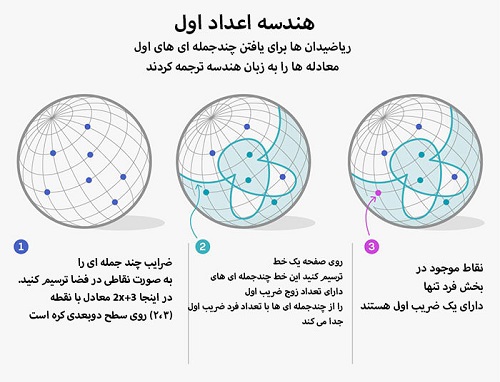
برای درک هندسه در میدانهای متناهی، یک چندجملهای را همارز یک نقطه در فضا درنظر بگیرید. ضرایب چندجملهای هم نقش مختصات مکانی را ایفا میکنند. برای مثال در میدان متناهی ۱، ۲ و ۳، چندجملهای ۲x+۳ در فضای دوبعدی در نقطهی (۲، ۳) قرار میگیرد.
اما حتی سادهترین میدان متناهی هم دارای تعدادی نامتناهی چندجملهای است. میتوان با افزایش اندازهی بزرگترین نما یا درجهی عبارت، چندجملهایهای دقیقتری ساخت. برای مثال چندجملهای x۲-۳x-۱ بهصورت یک نقطه در فضای سهبعدی نمایش داده میشود. چندجملهای ۳x۷+۲x۶+۲x۵-۲x۴-۳x۳+x۲-۲x+۳ بهصورت یک نقطه در فضای هشتبعدی نمایش داده میشود.
فضای هندسی در فرضیهی جدیدشامل کل چندجملهایها با یک درجهی مشخص برای یک میدان متناهی مشخص است. حالا این سؤال مطرح میشود: راهی برای جداسازی کل نقاط نمایشدهندهی چندجملهایهای اول وجود دارد؟ استراتژی ساوین و شوسترمان تقسیم فضا به دو بخش است. یکی از بخشها شامل تمام چندجملهایها با تعداد ضریب زوج و دیگری شامل چندجملهایها با تعداد ضریب فرد است.
به این ترتیب حل مسئله با تقسیمبندی یادشده آسانتر میشود. فرضیهی اعداد اول دوقلو برای میدانهای متناهی با ضریب یک صدق میکند (همانطور که عدد اول دارای یک ضریب مستقل یعنی خود آن عدد است)؛ و از آنجا که عدد ۱ فرد است میتوان بخشی از فضا با ضریبهای زوج را کاملا نادیده گرفت.
ترفند اصلی حل مسئله در تقسیم است. یک منحنی یکبعدی میتواند فضایی دوبعدی را به دو قسمت تقسیم کند. برای مثال خط استوا سطح زمین را به دو قسمت تقسیم میکند. به همین ترتیب میتوان فضاهای با ابعاد بالاتر را بهوسیلهی سطوحی با ابعاد کمتر تقسیم کرد.
از طرفی شکلهایی با ابعاد کمتر که فضاهای چندجملهای را تقسیم میکنند مانند استوا واضح نیستند. چنین اشیایی براساس فرمولی ریاضی به نام تابع موبیوس ترسیم میشوند که یک چندجملهای را بهعنوان ورودی دریافت میکند و در صورتی که تعداد ضریبهای اول چندجملهای زوج باشد، خروجی ۱، در صورتی که تعداد ضریبهای چندجملهای فرد باشد، منفی ۱ و در صورتی که صرفا دارای یک ضریب تکراری باشد صفر را برمیگرداند (برای مثال ۱۶ را میتوان بهصورت ۲*۲*۲*۲ به دست آورد).
چندجملهایها گزینهی مناسبی برای جستجوی اعداد اول هستند.
منحنیهایی که توسط تابع موبیوس ترسیم میشوند پیچیده و دارای چرخش زیاد هستند و خود را در بسیاری از نقاط قطع میکنند. تحلیل نقاط تقاطع که تکینگی هم نامیده میشوند کار دشواری است (زیرا متناظر با چندجملهایهایی با ضریب اول تکراری هستند). نوآوری اصلی ساوین و شوسترمان یافتن روشی دقیقی برای برش حلقههایی کم بعد به بخشهای کوتاهتر بود. طبیعتا بررسی بخشهای کوتاهتر آسانتر از بررسی حلقههای کامل است.
ساوین و شوسترمان پس از طبقهبندی چندجملهایها براساس تعداد ضریب اول فرد (سختترین مرحله)، باید مشخص میکردند کدام یک از چندجملهایها اول و کدام یک دوقلوی اول هستند. آنها برای رسیدن به این هدف از فرمولهای متعددی استفاده کردند که معمولا ریاضیدانها برای بررسی اعداد اول در میان اعداد طبیعی به کار میبرند. ساوین و شوسترمان از روش خود برای اثبات دو نتیجهی عمده دربارهی تعداد زیادی از زوج چندجملهایهای اول دوقلو با تفاضل مشخص استفاده کردند.
علاوه بر این اثبات جدید تعداد دقیق چندجملهایهای اول قابل انتظار در میان چندجملهایهایی از یک درجهی مشخص را نمایش میدهد. این دستاورد هم ارز دستیابی به تعداد اعداد اول دوقلو در بازهای طولانی روی محور اعداد حقیقی است؛ نتیجهای رویایی برای ریاضیدانها. زیو رودنیک ریاضیدان میگوید: این اولین اثباتی است که قیاسی کمی از مقدار قابل انتظار روی بازهای از اعداد صحیح را نمایش میدهد و قبلا چنین نتیجهای به دست نیامده است.»
با وجود گذشت تقریبا ۸۰ سال از اثبات فرضیهی ریمان در منحنیهای میدان متناهی توسط آندره وی، ساوین و شوسترمان نشان دادند که این نظریه امروزه هم کاربرد دارد. امروزه ریاضیدانها پژوهش خود را روی فرضیهی ساوین و شوسترمان متمرکز کردهاند؛ این نظریه میتواند الهامبخش دانشمندان دیگر باشد.



رایانهها را میتوان به عنوان ابزارهای با ارزشی معرفی کرد که ریاضیدانها را در مسیر حل یک مساله ریاضی یاری میکنند، اما این ابزارها که روز به روز نیز هوشمندتر میشوند، میتوانند نقش بزرگتری را برای کشف و اثبات یک قضیهی ریاضی بر عهده گیرند.
استفاده از رایانهها برای اثبات مسائل ریاضی سابقهای بیش از ۴۰ سال دارد. اولین مسالهای که در آن از رایانه برای اثبات کمک گرفته شده، قضیهی چهار رنگ است. براساس قضیهی چهار رنگ برای رنگ آمیزی یک نقشه تنها وجود چهار رنگ کافی است و برای مثال در مورد نقشهی کشورها، میتوان به تمام کشور یک رنگ اختصاص داد، بدون اینکه دو کشور با رنگ یکسان در کنار هم قرار گیرند.
اثبات این قضیه برای اولین بار در سال ۱۹۷۶ میلادی با استفاده از رایانه ارائه شده، اما بعدها مشکلاتی در اثبات مورد نظر پیدا شد و اثبات صحیح این مساله تا سال ۱۹۹۵ تکمیل شد.
در سال ۲۰۰۳، توماس هی از دانشگاه پیتسبورگ اثباتی را برای قضیهی کپلر که در آن از یاری رایانهها کمک گرفته شده بود، منتشر کرد. قضیه یا حدس کپلر در پی آن است تا بهینهترین حالت ممکن برای قرار گرفتن تعداد حداکثری اشیا با فرم کره را در یک فضای اقلیدسی ارائه کند. قضیه کپلر به زبان ساده بهینهترین روش چیدن پرتقال روی یکدیگر به گونهای است که در میوه فروشیها چیده میشود.
اگرچه توماس هی اثبات خود را در سال ۲۰۰۳ میلادی منتشر کرد، اما بسیاری از ریاضیدانها این اثبات را به دلیل حجم بالای آن و سخت بودن فرآیند صحیح بودن اثبات انجام شده، قبول نکردند، چراکه حجم اثباتی که هی با استفاده از رایانه به آن دست یافته بود، بیش از ۲ گیگابایت بود که در زمان خود حافظهی بسیار زیادی به شمار میرفت. اما هی ناامید نشده و با استفاده از یک اثبات تصدیق شده که با استفاده از رایانه به دست آمده بود، موفق به اثبات قضیه کپلر شد.

دانشمندان با استفاده از علم احتمال، مجموعهی حالاتی را که اعداد یک تا ۷٫۸۲۵ میتوانند رنگ متفاوتی به خود بگیرند را 102,300 حالت بیان کردهاند. این عدد از تعداد ذرات بنیادی که تاکنون در جهان هستی کشف شده نیز بیشتر است.
البته دانشمندان موفق شدهاند تا با استفاده از روشهای تقارن و تئوری اعداد، تعداد احتمالات موجود را به کمتر از یک تریلیون حالت کاهش دهند. برای آزمایش هر یک از حالات مورد نظر با استفاده از ابررایانهی Stampede متعلق به دانشگاه تگزاس که از وجود بیش از ۸۰۰ هسته پردازشی بهره میبرد، یک روز زمان نیاز است. ابررایانهی مورد نظر قادر است تا 1019 ریاضی را به انجام برساند.
شبکهی بزرگی از رایانهها در سطح جهان که با نام GIMPS (Great Internet Mersenne Prime Search) شناخته میشود، قادر است در هر ثانیه بیش از ۴۵۰ تریلیون عملیات ریاضی را انجام دهد. از این شبکهی رایانهای برای پیدا کردن بزرگترین عدد اول استفاده میشود. این شبکهی رایانهای قادر است پس از ۶ ساعت فعالیت به توان ابررایانهی تگزاس برسد.
این ابررایانه پس از انجام پردازش و تحلیل هر یک از حالتهای خود، اثبات خود را با حجم ۲۰۰ ترابایت ارائه کرد که با تقسیم آن به هر یک از انسانهای موجود روی زمین، به هر نفر ۳۰٫۰۰۰ بایت اطلاعات میرسد.
پیشرفتهای حاصل شده در دنیای فناوری به چه معنا است؟ آیا در آیندهی نزدیک باید ریاضیدانان را نیز همچون رانندگان تاکسی، فروشندگان کالا، رادیولوژیستها و سایر شغلهایی که ماهیتی نسبتا تکراری دارند، دچار روزمرگی و از بین رفتن بدانیم؟
به طور قطع پاسخ این سوال منفی است. ریاضیدانها همچون بسیاری از حرفههای دیگر، بهرهگیری از رایانهها را به عنوان روش جدیدی از انجام تحقیقات مورد استفاده قرار میدهند، بطوریکه که فرآیند جدید استفاده از رایانهها باعث تولید شاخهی جدیدی از این رشته با عنوان ریاضیات تجربی شده است که مزایا و نتایج آن بسیار گسترده است.
اما ریاضیات تجربی به چه معنا است؟ بهترین تعریف برای ریاضیات تجربی را میتوان به کار گرفتن رایانهها به عنوان آزمایشگاهی برای تحقیقات عنوان کرد. برای مثال در رشتهها نظیر شیمی، فیزکی، زیست شناسی و مهندسی نیز برای انجام آزمایشها و مدلسازی از وجود رایانهها استفاده کرده و فرضیههای خود را با استفاده از این ابزار و براساس راههای مشخص و مرسوم اثبات میکنند.
البته از یک نظر ریاضیات تجربی مفهوم چندان جدیدی بصورت بنیادی نیست. دانشمند بزرگ یونانی، ارشمیدس در قرن سوم پیش از میلاد در این خصوص چنین اظهار نظر کرده است:
ریاضیات تجربی مبتنی بر فناوریهای رایانهای در کنار خود تکنولوژی را به خدمت گرفتهاند. با گذشت هر سال و تقویت بیش از پیش قدرت سختافزاری رایانههای مورد استفاده بسیاری از نرمافزارهای مورد استفاده برای انجام محاسبات ریاضی نظیر Maple، Mathematica، Saga و سایر گزینههای موجود بیش از پیش تقویت میشوند.
هرچند استفاده و وجود اثباتهای مبتنی بر دانش انسانی ضروری به نظر میرسد، اما رایانهها نیز برای یاری ریاضیدانان به منظور اثبات تئوریهای جدید و ارائهی استنتاج قوی، در حال پیشرفت و در دست گرفتن امور هستند.
البته در مقام مقایسه، اثباتهای ارائه شده توسط رایانهها بسیار متقاعد کننده و صحیح هستند، چراکه انسان به دلیل برخورداری از ذاتی خطاپذیر، بعضا اثباتهایی را ارائه کرده که دچار مشکلاتی بوده و خواهند بود، هرچند در رایانهها به دلیل اینکه ماشین از قوانین خاصی پیروی میکند، امکان بروز خطا به خودی خود ممکن نیست.
برای مثال میتوان به پیدا کردن بزرگترین اعشار عدد پی اشاره کرد که توسط آلکساندر یی و شیجرو دو انجام شده و تا ۱۲.۱ تریلیون رقم از عدد پی را پیدا کردهاند. این دو دانشمند پس از پایان یافتن عملیات، بخشی از محاسبات خود را با یک الکوریتم دیگر که به صورت کامل متفاوت بود، انجام دادند و پس از آنکه مشخص شد نتایج به دست آمده با نتیجهی روش اول در موارد آزمایش یکی است پی به صحیح بودن روش مورد استفاده بردند.
با پیشرفت علوم رایانهای و ترکیب هر چه بیشتر آن با تحلیلهای ریاضی دانشمندان، ریاضیدانان برای سپردن بخشی از فرآیند اثبات مسائل ریاضی مشکل نداشته و پروسه اثبات مسائل بسیار راحتتر از پیش خواهد شد.
دانشمندان بلند پایهی دنیای ریاضی معتقدند که با وجود پیشرفت روزافزون اثباتهای ریاضی در سالهای آینده، همچنان بخش زیادی از این فرآیند توسط دانشمندان و متخصصان ریاضی انجام خواهد شد.

امروزه ریاضیات محض وابستگی شدیدی به محاسبات نرمافزاری پیدا کرده است. حتی برخی از بزرگترین نوابغ این علم نیز این روزها برای درک و اعتبارسنجی اثباتهای خود ناگزیر شدهاند که به نرمافزارها روی آورند.
کوین بازارد، نظریهپرداز عددی و استاد ریاضی محض از کالج سلطنتی لندن بر این باور است، زمان آن رسیده که عصر جدیدی در ریاضیات را برمبنای اثبات رایانهسازیشده آغاز کنیم. بزرگترین اثباتهای فعلی بهحدی پیچیده هستند که عملا هیچ بشری نمیتواند جزئیات آن را درک کند؛ چه رسد که بخواهد آن را اعتبارسنجی کند. بازارد از این موضوع نگران است که بسیاری از اثباتهایی که ما پیش از این، آنها را کاملا صحیح میپنداشتیم، اساسا غلط از آب درآیند. از این رو، ریاضیدانان به کمک نیاز دارند.
اما اثبات» چیست؟ اثبات بهمعنای نشاندادن درستی یک گزارهی ریاضیاتی است. با یادگیری تکنیکهای جدید اثبات، ما قادر به درک ریاضیات خواهیم شد و نتایج این علم نهایتا در بسیاری از زمینههای دیگر علمی بهکار گرفته خواهد شد.

برای تولید یک اثبات، باید کار را با معانی آغاز کنیم. برای مثال، مجموعه اعداد صحیح را در نظر بگیرید؛ مجموعهای متشکل از تمام اعداد صحیح از منفی بینهایت تا مثبت بینهایت. این مجموعه را بهشکل .، ۱،۲، ۰، ۱-، ۲-،. بنویسید. سپس نظریهای را مطرح کنید؛ برای مثال، بگویید بزرگترین عدد صحیح وجود ندارد.» اثبات این نظریه متشکل از یک استدلال منطقی خواهد بود که نشان دهد این نظریه صحیح یا غلط است (که درمورد گزارهی اخیر صحیح است). مراحل منطقی در این اثبات هر یک بر مبنای حقایق ازپیش اثباتشدهای تعریف خواهد شد که قبلا درستی آنها را پذیرفتهایم؛ حقایقی از این دست که عدد یک کوچکتر از دو است.»
اثباتهای جدید مطرحشده ازسوی ریاضیدانان حرفهای معمولا بر پایهی یک مجموعه نتایج اثباتشده تعریف میشوند که پیشتر درستی آنها درک شده است. اما بازارد میگوید در بسیاری از موارد، حتی درستی اثباتهایی که اساس اثباتهای بعدی قرار میگیرند نیز به روشنی درک نمیشود. برای مثال، مقالات چشمگیری وجود دارند که در آن به نتایج تحقیقاتی ارجاع داده شده که هنوز منتشر نشدهاند. این همان چیزی است که بازارد را نگران کرده است. او در حاشیهی دهمین کنفرانس اثبات تعاملی نظریات در پرتلند آمریکا میگوید:
من ناگهان درمورد درستی بسیاری از نشریات ریاضیاتی احساس نگرانی کردم؛ چراکه ریاضیدانان معمولا جزئیات را بررسی نمیکنند و من قبلا نیز غلطبودن برخی را به چشم دیدهام.
او در خلال یکی از اسلایدهای ارائهی خود در کنفرانس این موضوع را یادآور شده است: گمان میکنم شانس اینکه برخی از مهمترین کاخهای ما روی شن بنا شده باشند، صفر نیست؛ هرچند که این شانس کم است.»
در ریاضیات جدید باید همهچیز از نو اثبات شود. تمامی مراحل یا دستکم استدلالهای مطرحشده باید بهدقت چک شوند. از سوی دیگر، هنوز کارشناسانی زُبده و بزرگانی از جامعهی ریاضی حضور دارند که یک راهنمای مطمئن برای اعتبارسنجی گزارههای صحیح و غلط ارائه کردهاند. از این رو، اگر یکی از پیشگامان علم ریاضی به مقالهای ارجاع داده و از نتایج آن در مقالهی خود استفاده کرده باشد، پس احتمالا نیازی به بررسی اعتبار اثباتهای مطرحشده در آن منابع نخواهد بود.
از دیدگاه بازارد، ریاضیات مدرن بیش از حد به منابع گذشته وابسته شده است؛ موضوعی که علت آن به پیچیدگی زیاد نتایج بازمیگردد. در یک اثبات جدید ممکن است به ۲۰ مقالهی قدیمیتر ارجاع شده باشد و هر یک از این ۲۰ مقاله ممکن است خود دربرگیرندهی هزاران صفحه استدلالهایی فشرده باشد. در این میان، اگر یک ریاضیدان مجرب یک مقالهی هزار صفحهای را بنویسد یا حتی تنها بدان ارجاع کند، ریاضیدانان دیگر ممکن است تصور کنند که آن مقالهی ۱۰۰۰ صفحهای (بههمراه اثبات جدید) همگی صحیح هستند و درنتیجه، به خود زحمت بررسی دوبارهی آن را ندهند. این در حالی است که ریاضیات باید برای همگان قابلاثبات باشد و نه صرفا برای تعدادی انگشتشمار کارشناس خبره.
این وابستگی بیش از اندازهی ما به مقالات گذشته باعث بروز نوعی شکنندگی در درک حقیقت شده است. برای مثال، اثبات آخرین نظریهی فرمات را در نظر بگیرید. این اثبات در سال ۱۶۳۷ ارائه شد و در کتاب رکوردهای جهانی گینس نیز نام آن بهعنوان دشوارترین مسئلهی ریاضی» به ثبت رسیده است. بازارد ادعا میکند که در واقع هیچکس بهدرستی نتوانسته این اثبات را کاملا درک کند و بدتر اینکه شاید کسی حتی از درستی آن نیز مطمئن نباشد. او میگوید:
به باور من، هیچ انسانی، زنده یا مرده، جزئیات اثبات نظریهی آخر فرمات را نمیداند؛ با این حال، جامعه درستی آن را پذیرفته است؛ چرا که این اثبات بنابر حکم پیشکسوتان صحیح بوده است.

چند سال پیش، بازارد در خلال گفتوگویی میان دو تن از زبدگان علم ریاضی با نامهای توماس ها و ولادیمیر ووسفکی، با مفهوم اعتبارسنجی نرمافزاری اثبات» آشنا شد. با کمک چنین نرمافزاری میتوان اثباتها را بهشکلی سیستماتیک و از طریق رایانه اعتبارسنجی کرد. این موضوع میتوانست بهمنزلهی پایانی بر عصر سلطهی پیشکسوتان و آغاز دموکراسیزاسیون حقایق علم ریاضی باشد.
این نرمافزار اعتبارسنجی اثباتها، لین (Lean) نام داشت. بازارد بهمحض شروع استفاده از لین، جذب کاربردهای شگفنانگیز آن شد. این نرمافزار نهتنها باعث شد بازارد بتواند اثباتها را بدون هرگونه چونوچرایی اعتبارسنجی کند؛ بلکه باعث شد یک تفکر شفاف و خللناپذیر درمورد ریاضیات درون وی شکل بگیرد. او میگوید:
من فهمیدم که رایانهها تنها ورودیهایی با دقت بسیار بالا را قبول میکنند. این همان روش تفکراتی موردعلاقهی من در ریاضیات است. من عاشق آن شدم؛ چراکه حس کردم نیمهی گمشدهی خود را در آن یافتهام. من چیزی را یافتم که آنگونه درمورد ریاضیات میاندیشید که خود میاندیشیدم.
برای آنکه بتوان یک اثبات را بهوسیلهی لین اعتبارسنجی کرد، کاربر باید آن اثبات را فرمولبندی کند؛ یعنی آن را از شکلوشمایل زبانها و نمادهای انسانی به زبان برنامهنویسی لین ترجمه کند. کاربر همچنین باید تمامی تعاریف و اثباتهای جانبی مطرحشده در آن اثبات را نیز فرمولبندی کند. ناگفته پیداست که چنین فرایندی وقت و انرژی زیادی میگیرد؛ با این حال، برتری لین در آن است که میتواند از پس تمامی گزارههای ریاضی ورودی برآید؛ موضوعی که درمورد سایر برنامههای دستیار اثبات صادق نیست.
جامعهی روبه رشد ریاضی جهان، بهویژه در بخش آموزش، از معرفی نرمافزار لین استقبال کرده است.جرمی اویگاد، استاد علوم نظریهی اثبات در دانشگاه کارنگی ملون است. او و بازارد هر دو نرمافزار لین را در کلاسهای مقدماتی آموزش اثبات معرفی کردهاند. نرمافزار صحت اثبات را خط به خط بررسی میکند و بازخوردها را نیز گزارش میدهد. چنین ویژگیهایی برای دانشآموزان بسیار مفید واقع خواهد شد.
آویگاد از استقبال جامعهی علمی بسیار خشنود به نظر میرسد، اما هشدار میدهد که این فناوری هنوز نیاز به توسعهی بیشتری دارد. استفاده از نرمافزارهای دستیار در اثبات میتواند بسیار وقتگیر باشد. او میگوید با اینکه چیزی حدود چند دهه از معرفی این ایده میگذرد و پیشرفتهای زیادی نیز حاصل شده است، ولی هنوز به نقطهی مطلوب نرسیدهایم.
بازارد معتقد است که درصورت حل چالشهای پیش رو، نرمافزار لین میتواند آثاری فراتر از حوزهی اثبات داشته باشد. برای مثال، مشکل جستوجو را در نظر بگیرید. هر ساله حجم بسیار بالایی از رساله در جهان منتشر میشود. در چنین آشفتهبازاری، دسترسی به یک روش مناسب برای جستوجو در میان اثباتها بسیار حائر اهمیت خواهد بود. هی و بازارد میگویند که اگر بتوانیم چکیدهی تمامی مقالات جدید را وارد نرمافزار کنیم، هر ریاضیدانی میتواند با جستوجو در بانک دادهی نرمافزار، هر مقالهای را بههمراه تمامی اطلاعات مربوط به آن بیابد. این بهمعنای دسترسی به قدرت بینظیر مغز پیشکسوتان ریاضی تنها از طریق یک نرمافزار خواهد بود.

دانشمندان علوم رایانه میتوانند از این بانک دادهی عظیم برای آموزش هوش مصنوعی بهره ببرند. از آنجا که نتایج بهدستآمده از چنین بانک دادهای به زبان خود لین نگاشته شدهاند؛ بنابراین پردازش این نوع اطلاعات برای یک رایانهی دیگر نیز بسیار آسانتر خواهد بود. هدف غایی دانشمندان، تولید یک ماشین خودکار عمومی باهدف اثبات نظریات است؛ نرمافزای که بتواند اثباتهای مختصبه خود را تولید کند و محاسبات ریاضیاتی را خود انجام دهد. اثباتکنندههای خودکار به همان فناوریای تکیه خواهند داشت که امروزه لین برای اعتبارسنجی اثباتها بهکار گرفته است. افزایش مقبولیت نرمافزاری مانند لین میتواند نهایتا گامی مؤثر در مسیر اتوماسیون کل ریاضیات بهشمار آید.
مرکز هلیکس واقع در شمال شرق منهتن قرار است پنجم اکتبر سال جاری میزبان نشستی با موضوع اتوماسیون ریاضیات باشد. در این رویداد که بهصورت زنده ازطریق کانال یوتیوب و وبسایت آن پوشش داده خواهد شد، مایکل هریس، استاد ریاضی دانشگاه کلمبیا و از همکاران بازارد حضور خواهد داشت.
کی از دغدغههای هریس آن است که دانشمندان علوم رایانه و شرکتهای فناوری انگیزههای یکسانی برای همکاری با ریاضیدانان در اتوماسیون ریاضی نداشته باشند. برای مثال، دانشمندان علوم رایانه احتمالا تمایل دارند که از فناوری لین برای کسب اطمینان از بینقص بودن برنامههای خود بهره ببرند، شرکتهای فناوری درصدد سودآوری هستند و از آن سو، ریاضیدانانی نظیر بازارد تنها در اندیشهی ارتقاء دانش ریاضیات هستند. هریس میگوید:
یکی از پیشبینیهای من این است که اگر افراد نخبهای مانند توماس هی و بازارد به حرکت خود در این مسیر ادامه دهند، یک نتیجهی خارقالعاده در انتظار خواهد بود؛ این نتیجه نهتنها میتواند یک هوش مصنوعی، بلکه شاخهای کاملا جدید از ریاضیات یا روشی جدید برای فکرکردن باشد.

فرض کنید بین نه نفر برای خرید بستنی وانیلی و شکلاتی رأیگیری شود و ۵ نفر از ۹ نفر بستنی شکلاتی را انتخاب کنند؛ بنابراین خواست اکثریت بستنی شکلاتی خواهد بود تا زمانی که تعداد انتخابها دو مورد باشد، مشکل خاصی در تعیین نظر اکثریت وجود ندارد.

فرض کنید انتخاب سومی مانند بستنی توتفرنگی اضافه شود. آنگاه سه حالت برای یک فرد اتفاق میافتد؛ یا بستنی توتفرنگی در ارجحیت سوم و آخر قرار دارد؛ یا در مکان دوم قرار دارد؛ یا ارجحیت اول فرد است که بدین ترتیب انتخاب اولش تغییر میکند و بستنی توتفرنگی میشود.
در مثال قبلی فرض کنید هر چهار نفری که انتخابشان وانیلی بوده و سه نفر از افرادی که انتخابشان شکلاتی بوده است، بستنی توتفرنگی ارجحیت آخر آنها باشد و فقط دو نفر از افرادی که انتخابشان شکلاتی بود، توتفرنگی انتخاب اولشان باشد. در نتیجه رأی خود را به بستنی توتفرنگی تغییر بدهند. اتفاقی که رخ میدهد این است که رأی ۴ نفر وانیلی و ۳ نفر شکلاتی و ۲ نفر توتفرنگی میشود در نتیجه وانیلی بهعنوان خواست اکثریت انتخاب میشود.
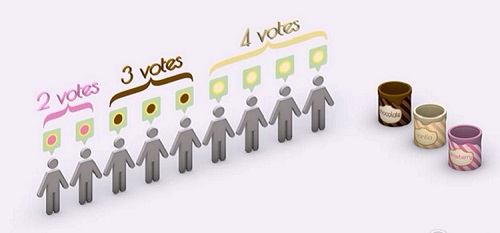
در واقع تأثیر انتخاب سوم بدین گونه است که انتخاب سوم نادیده گرفته میشود و انتخاب گروه از شکلاتی به وانیلی تغییر پیدا میکند؛ درحالیکه میدانیم در این گروه، بستنی شکلاتی به وانیلی ارجحیت دارد و انتخاب شکلاتی اکثریت را خوشحال خواهد کرد. به این پدیده اثر ضایع کننده میگویند. در واقع بستنی توتفرنگی بدون اینکه خود شانس برد داشته باشد، شانس برد دیگری را ضایع کرده است. برای اینکه این پدیده رخ ندهد، ما باید سیستم رأیگیری خود را عوض کنیم. بنابراین از رأیگیری ترجیحی استفاده میکنیم؛ بدین معنی که هر فرد انتخابهای خود را بر اساس اولویت لیست میکند. بنابراین برای مثال قبل داریم:
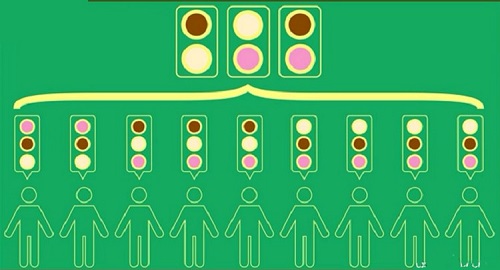
همانطور که از تصویر میتوان نتیجه گرفت، بین شکلاتی و وانیلی، اولویت با بستنی شکلاتی است. بین وانیلی و توتفرنگی، با وانیلی و در انتها بین شکلاتی و توتفرنگی با شکلاتی است. بنابراین انتخاب گروه به ترتیب شکلاتی، وانیلی و توتفرنگی است و بستنی شکلاتی بهعنوان خواست اکثریت انتخاب خواهد شد. در این مرحله بیایید مثال دیگری را با ۱۲ نفر رأیدهنده، توسط رأیگیری ترجیحی همانند تصویر زیر بررسی کنیم.
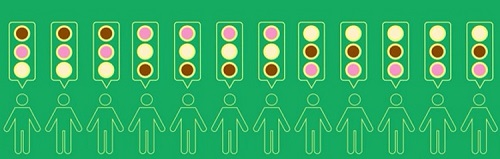
انتخاب اکثریت، شکلاتی نمیتواند باشد؛ چون اکثریت وانیلی را بر شکلاتی ترجیح میدهند. اما از طرف دیگر وانیلی نمیتواند باشد؛ چون اکثریت توتفرنگی را به وانیلی ترجیح میدهند و در نهایت توتفرنگی هم نمیتواند باشد؛ چون اکثریت شکلاتی را به آن ترجیح میدهند. مهم نیست انتخاب اکثریت را چه فرض کنیم؛ همیشه انتخاب دیگری هست که گروه را خوشحالتر کند. به نظر میرسد این گروه انتخاب ارجح ندارد. به این پدیده، ترجیح دوری یا پارادوکس کندورسه گفته میشود. برای اینکه بدانیم مشکل از کجا است، در نظر داشته باشید ترتیب ارجحیت گروه برای سه انتخاب، ۶ حالت دارد؛ اما بررسی دوبهدوی سه انتخاب، ۸ حالت ممکن دارد که دو حالت آخر در واقع پدیده ترجیح دوری را ایجاد میکنند.
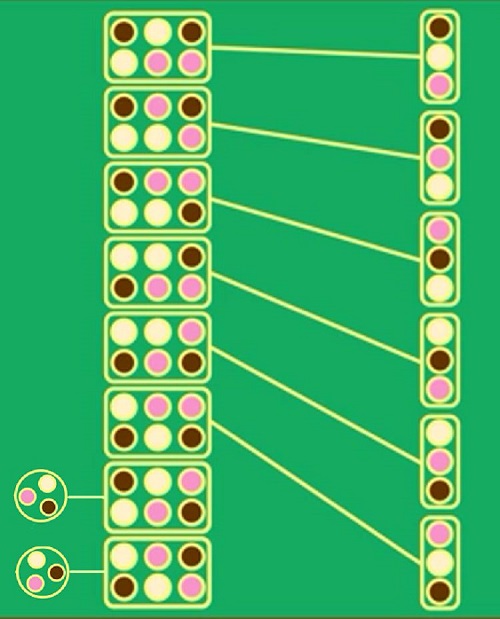
برای رفع این مشکل بیایید از سیستم رأیگیری حذفی استفاده کنیم. بدین صورت که ابتدا انتخابی که کمترین رأی را دارد، حذف میکنیم و سپس بین دو گزینه دیگر بررسی را انجام میدهیم. در این مثال بستنی شکلاتی با سه انتخاب حذف میشود و بین دو انتخاب دیگر بستنی توتفرنگی با نتیجه ۷ به ۵ برنده خواهد شد. در رأیگیری حذفی، پدیدهی ترجیح دوری اتفاق نمیافتد و همیشه یک برنده داریم. اما همانند گذشته، سیستم رأیگیری جدید با اینکه مشکلات ما را رفع کرده است، اما دارای ایراداتی بسا عجیبتر هست.
مثالی را با ۱۷ نفر در نظر بگیرید که انتخابهای آنها بهصورت تصویر زیر باشد.

با استفاده از رأیگیری حذفی بستنی وانیلی با ۵ انتخاب حذف میشود و بین دو انتخاب دیگر، بستنی شکلاتی با ۱۱ رأی در مقابل ۶ رأی از بستنی توتفرنگی میبرد. اما فرض کنید قبل از خرید بستنی، گفته شود اگر انتخاب گروه بستنی شکلاتی باشد به هر فرد یک عدد آبنبات هم داده خواهد شد. با توجه به این گفته فرض کنید دو تا از افرادی که انتخابشان توتفرنگی بود، متقاعد شدند که بستنی شکلاتی را در ارجحیت قرار بدهند.

دقت کنید بستنی شکلاتی از قبل بهعنوان ارجحیت این گروه انتخاب شده بود و عوض شدن انتخاب دو نفر به بستنی شکلاتی در جهت افزایش خواست گروه نسبت به بستنی شکلاتی است؛ اما نتیجهی فرایند رأیگیری متفاوت خواهد بود، این بار بستنی توتفرنگی با ۴ انتخاب حذف و بستنی وانیلی با ۹ رأی از ۱۷ رأی برنده میشود. در واقع با اینکه انتخاب اول نسبت به بستنی شکلاتی بیشتر شده؛ اما بستنی شکلاتی به علت انتخاب بیش از حد باخته است! به این پدیده شکست یکنواختی گفته میشود.
این یکی از مثالهایی است که نشان میدهند اگرچه ممکن است در یک گروه، هر فرد بهصورت مستقل رفتارهای معقولانهای بروز دهد؛ اما گروه بهعنوان یک کل میتواند رفتاری کاملا عجیب از خود نشان دهد.
به پدیدههای ذکرشده، پارادوکسهای رأیگیری گفته میشود و هر کدام نشان میدهد که انتخابهای گروهی چقدر متفاوت نسبت به انتخابهای فردی میتوانند رفتار کنند. شاید تصور شود که این موارد ایرادات فنی هستند و سیستم رأیگیری ایدهآل وجود دارد که در هر شرایطی عاری از این مشکلات باشد. اما در اوایل دهه ۵۰ میلادی، اقتصاددان آمریکایی کنت ارو نشان داد پارادوکسهایی همانند موارد بالا اجتنابناپذیر هستند. به زبان ریاضی، هیچ سیستم رأیگیری وجود ندارد که ارجحیت فردی را به ارجحیت یک گروه مرتبط کند و عاری از پارادوکسهای رأیگیریِ شناختهشده باشد.
وقتی هر فرد یک رأی میدهد، در راستای انتخاب یک نوع بستنی کمک میکند. اما وقتی یک سیستم رأیگیری را انتخاب میکنیم در واقع از میان پارادوکسهای رأیگیری موجود یکی را انتخاب کردهایم. این موضوع محدودیتهای تصمیمگیری گروهی را نشان میدهد که با عنوان قضیهی عدم امکان ارو شناخته میشود. کنت ارو بعدها به خاطر این نتیجه، برنده نوبل اقتصاد شد. نتیجهای که باعث پیدایش نظریه انتخاب اجتماعی مدرن شد؛ بخشی از ریاضی که چگونگی تصمیمگیری گروهها را بررسی میکند.
رأیگیری یکی از ارکان جداییناپذیر زندگی اجتماعی مدرن است؛ اما عدم وجود یک سیستم رأیگیری ایدهآل شاید یکی از دیگر مواردی است که عدم وجود یک دنیای ایدهآل را نشان میدهد
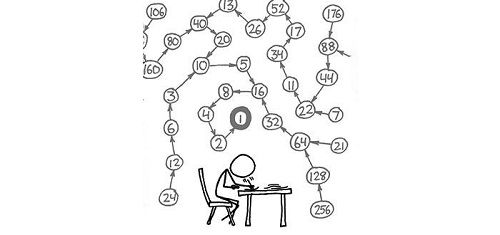
یک عدد طبیعی انتخاب کنید؛ اگر زوج بود آن را بر ۲ تقسیم کنید و اگر فرد بود آن را ۳ برابر کنید و با ۱ جمع ببندید؛ برای عدد جدید بهدستآمده همین فرایند را تکرار کنید؛ اگر این کار را ادامه دهید، در نهایت به عدد ۱ خواهید رسید؛ بهعنوان مثال:
۷→۲۲→۱۱→۳۴→۱۷→۵۲→۲۶→۱۳→۴۰→۲۰→۱۰→۵→۱۶→۸→۴→۲→۱
این موضوع در سال ۱۹۳۷ توسط لوتار کولاتز مطرح شد و کماکان بعد از گذشت چندین دهه، حلی برای آن در دسترس نیست. درستی این حدس تا عدد ۲۶۰ توسط کامپیوتر بررسی شده است؛ اما هنوز اثباتی برای آن وجود ندارد.

همانطور که میدانید عدد اول، عددی است که تنها بر ۱ و خودش بخشپذیر باشد. اعداد اولی که با همدیگر ۲ واحد اختلاف دارند، اعداد اول دوقلو نامیده میشوند؛ مانند (۳٬۵) یا (۱۱٬۱۳).
بزرگترین اعداد اول دوقلوی کشفشده که دارای ۳۸۸,۳۴۲ رقم هستند؛ برابرند با:
این اعداد در سپتامبر ۲۰۱۶ کشف شدند. تعداد جفتهای اعداد دوقلو تا عدد ۱۰۱۸ برابر است با ۸۰۸۶۷۵۸۸۸۵۷۷۴۳۶. آیا تعداد اعداد اول دوقلو نامتناهی است؟ سؤالی که تاکنون بیپاسخ مانده است. اعداد اول سهقلو به سه عدد فرد متوالی گفته میشود که هر سهی آنها اول باشند؛ تنها اعداد اول سهقلو (۳٬۵٬۷) هستند، چرا؟
یکی از معروفترین و قدیمیترین مسائل حلنشده در ریاضیات، حدس گلدباخ است که با وجود صورت بسیار سادهای که دارد، حدود ۲۷۰ سال ذهن ریاضیدانها را به خود مشغول کرده است. آرزوی هر ریاضیدانی این است که آن را حل کند و چهبسا برای رسیدن به حل آن همچون فیلم اتاق فِرما» دست به هر کاری بزنند! حدس گلدباخ بیان میکند که هر عدد صحیح زوج بزرگتر از ۲ را میتوان بهصورت مجموع دو عدد اول نوشت.» بهعنوان مثال:
۴=۲+۲
۶=۳+۳
۸=۵+۳
این حدس در سال ۱۷۴۲ میلادی توسط کریستین گلدباخ در نامهای به لئونارد اویلر مطرح شد. تلاشهای بسیاری در اثبات این حدس انجام شده است؛ تلاشهایی که منجر به کشف قضیههای دیگر شدهاند؛ اما این حدس کماکان حلنشده باقی مانده است. در سال ۱۹۹۲ مؤسسهی انتشاراتی مشهور Faber & Faber کتاب داستان پرفروشی با عنوان عمو پتروس و حدس گلدباخ» منتشر کرد که در آن، تاریخ ریاضیات در قالبی جذاب و داستانی شرح داده شده است. بعد از چند سال، انتشارات مزبور به منظور تبلیغ برای فروش بیشتر، جایزهای یک میلیون دلاری برای کسی که از تاریخ ۲۰ مارس ۲۰۰۰ ،حداکثر به مدت دو هفته موفق به اثبات حدس گلدباخ شود، تعیین کرد؛ اما تا اتمام تاریخ مقرر و پس از آن، تاکنون هنوز هیچ ریاضیدانی از پس اثبات این حدس بهظاهر آسان، برنیامده است. در سال ۲۰۱۴ توسط کامپیوتر نشان داده شد که این حدس برای اعداد زوج کوچکتر از ۱۰۱۸×۴ درست است؛ اما هر چقدر این بررسی جلو برود، کافی نخواهد بود و در انتها تنها چارهی ما تلاش برای اثبات آن است.
![]()
دکارت گفت اعداد کامل همچون انسانهای کامل، کمیاب هستند.» عدد کامل عددی است که برابر جمع مقسومعلیههای به غیر خودش باشد؛ بهعنوان مثال مقسومعلیههای ۶ به غیر خودش؛ ۱،۲،۳ هستند و داریم: ۶=۳+۲+۱. چند عدد کامل ابتدایی عبارتند از: ۲۸؛ ۴۹۶؛ ۸۱۲۸؛ ۳۳۵۵۰۳۳۶.
در ژانویهی سال ۲۰۱۶، چهل و نهمین عدد کامل کشف شد؛ این عدد دارای ۴۴,۶۷۷,۲۳۵ رقم است و مقدار آن برابر است با:
از ویژگیهای جالب اعداد کامل این است که آنها را میتوان بهصورت جمع اعداد طبیعی متوالی یا جمع مکعب اعداد فرد متوالی نوشت. همچنین هر عدد کامل زوج، حتما به ۶ یا ۸ ختم میشود.
همچنان این سؤالها که آیا عدد کامل فرد وجود دارد؟» و آیا تعداد اعداد کامل نامتناهی است؟» بیپاسخ ماندهاند.
به نظر شما آیا عددی وجود دارد که مساوی با دو برابر جمع مقسومعلیههای به غیر از خودش باشد؟ نترسید! این سؤال حل شده است و پاسخش را به عهدهی خودتان میگذاریم. به این عدد، عدد کامل از مرتبهی سه گفته میشود.

این حدس بیان میکند بین مجذور هر دو عدد طبیعی متوالی، حداقل یک عدد اول وجود دارد». این مسئله در سال ۱۹۱۲ توسط لژاندر بیان شد و حدود صد سال است که برای آن اثباتی پیدا نشده است. جالب است بدانید حل این حدس اگرچه منجر به حل فرضیه ریمان نمیشود؛ اما قویتر از یکی از نتایج فرضیهی ریمان است.

همانطور که میدانید به عددی گنگ گفته میشود که نتوان آن را بهصورت کسری نوشت یا به عبارت سادهتر؛ وقتی بهصورت اعشاری نوشته شود، دارای الگوی مشخصی نباشد. اثبات گنگ بودن عددی مانند رادیکال ۲ راحت است. اما در حالت کلی اثبات گنگ بودن یک عدد، مسئلهی سختی به شمار میرود؛ بهعنوان مثال اثبات گنگ بودن عدد پی در قرن ۱۸ توسط لمبرت و بعد از اثبات گنگ بودن عدد نپر اتفاق افتاد. اما تاکنون اثبات نشده است که π+e و πe گنگ هستند یا خیر.
نکتهی جالب در مورد این موضوع آن است که ما میدانیم حداقل یکی از دو عبارت فوق گنگ است اما کدام یک؟
حدس اردیش-استراوس در سال ۱۹۴۸ توسط دو ریاضیدان به همین نام ارائه شد؛ این حدس بیان میکند هر عدد گویا بهصورت ۴ بر روی n را میتوان بهصورت جمع سه کسر به شکل زیر نوشت:»
به عنوان مثال:
درستی این حدس توسط کامپیوتر تا عدد ۱۰۱۷ تائید شده است؛ اما کماکان اثباتی برای آن وجود ندارد.
شاید صورت سادهی بعضی از این مسائل شما را نیز به فکر حل آنها یا طرح سؤال حلنشدهای به نام خودتان انداخته باشد. مطمئنا روزی این مسائل حل خواهند شد، حتی اگر این تلاش همچون قضیهی اخر فرما ۳۵۸ سال طول بکشد. اما در انتها همواره سؤالهای حلنشدهای هستند که ذهن پرسشگر انسان را به چالش بکشند.

بسیاری بر این باورند که عدد پی (π) بهخاطر دقت محاسباتی بیپایان آن، احتمالا لایق عنوان شگفتانگیزترین عدد دنیای ریاضیات خواهد بود؛ اما بهعقیدهی ریاضیدانان، اعداد طلایی و ناشناختهی دیگری نیز وجود دارند که هرگز کم از رقیب دیرین خود ندارند.
اگر از شیفتگان دنیای ریاضیات هستید، پس احتمالا روز ۱۴ مارس (برابربا ۲۳ اسفند) بهگوشتان آشناست. این روز، بهعنوان روز جهانی شگفتانگیزترین و غیرمعقولترین عدد دنیا یعنی عدد پی (π) شناخته میشود. اما این عدد چیست؟ پی را بهسادگی میتوان نسبت محیط یک دایره به قطر آن دانست. این عدد را هرگز نمیتوان کاملا بهصورت اعشاری نوشت. شگفتانگیزتر آنکه پی، یک عدد متعالی یا غیرجبری است؛ بدینمعنا که هیچ معادلهی چندجملهای با ضرایب گویا را نمیتوان یافت که ریشهی آن عدد پی باشد.

اما این عدد در خیل عظیم اعداد شگفتانگیز طبیعت یک استثنا نبوده و نیست. برای بسیاری از ریاضیدانان، اعداد جالبتری وجود دارد که نسبتبه ثابت دایره، از جذابیت بالاتری برخوردار هستند. در اینجا سعی کردهایم فهرستی از اعداد شگفتانگیزی را برایتان نقل کنیم که از نگاه ریاضیدانان دستکمی از عدد پی ندارند.

فکر میکنید چهچیزی میتواند جذابتر از یک عدد پی باشد؟ شاید مسخرهترین پاسخ این باشد که بگوییم: دو تا عدد پی! ولی این واقعیت دارد. عدد تاو یا دور (Tau)، مقداری معادلبا دوبرابر مقدار پی است؛ یعنی چیزی در حدود ۶.۲۸.
جان بائز، ریاضیدانی از دانشگاه کالیفرنیا در ریورساید میگوید:
استفاده از تاو میتواند نسبتبه پی، فرمولها را برایمان واضحتر و منطقیتر کند. تمرکز بیشتر ما روی عدد π نسبتبه 2π، تنها ناشی از یک اتفاق تاریخی است.
بائز میگوید درحقیقت، تاو آن عددی است که در مهمترین فرمولهای ما دیده میشود. پی درواقع ارتباط میان محیط و قطر آن را مشخص میکند، درحالیکه تاو، بیانگر ارتباط میان محیط دایره و شعاع آن است و نکته اینجا است که بسیاری از ریاضیدانان بر این عقیدهاند که رابطهی دوم بسیار مهمتر است. عدد تاو به معادلاتی ظاهرا غیرمرتبط ظاهری متقارن میبخشد؛ معادلاتی نظیر مساحت دایره یا معادلات توصیفگر انرژی جنبشی و کشسانی.
اما در سالگرد گرامیداشت عدد پی، قرار نیست عدد تاو بهدست فراموشی سپرده شود. بنابر تصمیمگیری انجامگرفته ازسوی مؤسسهی فناوری ماساچوست، تاو نیز روز مخصوصبه خودش را خواهد داشت: ۲۸ ژوئن.

عدد جالب دیگری که در اینجا قصد معرفی آن را داریم، پایهی لگاریتم طبیعی یا بهاختصار عدد e است که ریاضیدانی سوئیسی لئونارد اویلر در قرن ۱۸ میلادی آن را کشف کرد. این عدد شگفتآور با مقدار تقریبی ۲.۷۱۸، ممکن است بهاندازهی عدد پی شهرت نداشته باشد؛ ولی عدد e نیز مانند رقیب خود، دارای یک روز مخصوصبهخود است. اهالی علم، روز ۷ فوریه را برای گرامیداشت این عدد عجیب انتخاب کردهاند.
پایهی لگاریتم طبیعی اغلب در معادلات مربوطبه لگاریتمها، رشد نمایی و اعداد مختلط استفاده میشود. کیت دولین، مدیر پروژهی ریاضی اوتریچ دانشگاه استنفورد در دانشکده تحصیلات تکمیلی بر این باور است که:
[این عدد] تعریف فوقالعادهای دارد که بنابر آن، تابع نمایی y=e^x در هر نقطه مقداری برابر با شیب خود دارد. بهعبارت دیگر، اگر مقدار یک تابع در یک نقطه برابر با ۷.۵ باشد، میزان شیب (یا مشتق) آن در آن نقطه نیز برابر با ۷.۵ خواهد بود. این عدد نیز درست مانند دیگر رقبای خود کاربرد فراوانی در ریاضیات، فیزیک و مهندسی دارد.
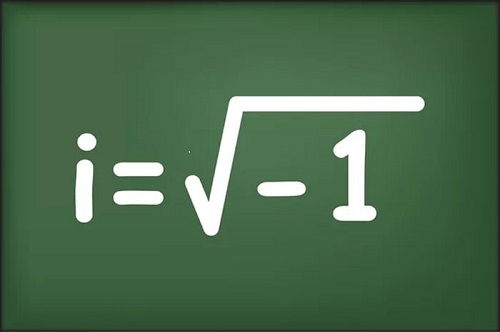
عدد شگفتانگیزی دیگری نیز وجود دارد که در غرابت کم از عدد پی ندارد: عدد i.
این عدد که جذر ۱- محسوب میشود، درحقیقت اصلا نباید وجود خارجی داشته باشد؛ چراکه اگر در خلال این سالها، اندک معلوماتی از قوانین پایهی ریاضیات در ذهنتان باقی مانده باشد، خوب میدانید که هرگز نمیتوان از اعداد منفی جذر گرفت.
یوجیبا چنگ، ریاضیدان دانشکده هنر شیکاگو اینگونه میگوید:
بااینحال، اگر ما این قانون را بشکنیم، قادر خواهیم بود اعداد موهومی را اختراع کنیم که همانند اعداد مختلط، اعدادی زیبا و درعینحال مفید هستند. دراینمیان، i یک عدد بهشدت عجیب است؛ چراکه عدد ۱- دارای دو ریشهی دوم است: یکی i و دیگری i-. اما درواقع نمیتوان تفاوت میان این دو ریشه را تشخیص داد. از اینرو، ریاضیدانان، تنها یکی از این ریشهها را بهعنوان i برگزیدند و دیگری را i-. این بسیار شگفت انگیز و خارقالعاده است.
بد نیست بدانید اعداد مختلط، اعدادی هستند که میتوان آنها را بهصورت مجموع دو بخش از عدد حقیقی و عدد موهومی بیان کرد.

شاید باور کردن آن سخت باشد که وضعیت عدد i میتواند حتی شگفتانگیزتر از آن چیزی باشد که اکنون به نظر میرسد. برای مثال، شما میتوانید عدد i را به بهتوان خود i برسانید. به عبارت دیگر، ریشهی دوم ۱- را بهتوان ریشهی دوم ۱- برسانید!
دیوید ریچسون، پروفسور ریاضیات در کالج دیکینسون در پنسیلوانیا و نویسندهی کتاب افسانههای غیرممکن: جستوجو برای حل مسائل ریاضی دوران باستان» (انتشارات دانشگاه پرینستون) میگوید:
در نگاه اول، این عدد ممکن است موهومیترین عدد ممکن بهنظر برسد؛ عددی موهومی که خود بهتوان عددی موهومی رسیده است. اما درحقیقت، همانطور که لئونارد اویلر طی مقالهای در سال ۱۷۴۶ نوشته است: این یک عدد حقیقی است!»
پیدا کردن مقدار واقعی i بهتوان i، نیازمند بازترکیب فرمول معروف اویلر براساس عدد گنگ e، عدد موهومی i و سینوس و کسینوس یک زاویهی مشخص است. هنگامی که فرمول یک زاویهی ۹۰ درجه را حل میکنیم ( که میتوان آن را بهشکل π/2 نیز نشان داد)، میتوان معادله را بهگونهای ساده کرد تا نشان دهد که i بهتوان i برابر است با e بهتوان 2/π-.
این محاسبات کمی گیجکننده بهنظر میرسد؛ بااینحال نتیجهی این معادله (در زاویهی ۹۰ درجه) نهایتا برابر خواهد بود با ۰.۲۰۷ که عددی کاملا حقیقی است. اگر حوصلهی سروکلهزدن با نحوهی این محاسبات را دارید، میتوانید به این آدرس سری بزنید. ریچسون میگوید:
همانطور که اویلر اشاره کرده، i بهتوان i دارای یک مقدار واحد نیست. بااینحال، رسیدن به این تعداد بینهایت از پاسخهای ممکن، بستگی به آن دارد که معادله را در چه زاویهای حل میکنید.
با این حجم پیچیدگی، بیدلیل نیست که نمیتوان به اختصاص یک روز خاص برای i بهتوان i» در آینده چندان امید بست.

عدد اول بلفیجور، عدد اولی واروخوانه است که بهصورت ۶۶۶ در میان ۱۳ عدد صفر و یک عدد یک در طرفین نوشته میشود (اعداد واروخوانه یا جناس قبل، به اعدادی اطلاق میشود که خواندن آن از دوطرف یکسان باشد). این عدد نحس (یا بهتعبیری شیطانی) را میتوان به شکل ۱۰۰۰۰۰۰۰۰۰۰۰۰۰۶۶۶۰۰۰۰۰۰۰۰۰۰۰۰۰۱ نوشت.
کلیف پیکاور، دانشمند و نویسندهای بود که این عدد شیطانی را بانام بلفیجور (یکی از دیوهای هفتگانهی دوزخ) نامگذاری کرد و شهرت فراوانی به آن بخشید.
این عدد ظاهرا نماد شیطانی مختصبه خودش را دارد که شبیه نماد وارونهی عدد پی است. مطابق با اطلاعات درجشده در وبسایت Pickover، این نماد از یک نشان دیدهشده در دستنوشتهی مرموز ووینیچ اقتباس شده است. این دستنوشتهی مشهور مجموعهای از تصاویر و متون عجیب است که گویی کسی از آن سر در نمیآورد.

دبلیو. هوگ وودین، ریاضیدانی از دانشگاه هاروارد سالهایی طولانی از وقت خود را صرف تحقیق درمورد اعداد بینهایت اختصاص داده است و بنابراین جای تعجبی هم نداشت که یکی از همین اعداد بینهایت را بهعنوان عدد دلخواهی خود انتخاب کند: 2aleph_0 یا ۲ بهتوان aleph-naught.
اعداد آلِف معمولا برای توصیف اندازهی مجموعههای نامحدود مورد استفاده قرار میگیرند (مجموعه، به هر دسته از اشیای متمایز در ریاضیات اطلاق میشود). یه این ترتیب، مثلا اعداد ۲، ۴ و ۶ میتوانند باهم یک مجموعه با اندازهی ۳ را تشکیل دهند. در مورد اینکه چرا وودین این عدد را انتخاب کرده، خود او میگوید:
اگر بتوانیم درک کنیم که 2aleph_0 برابر با خود aleph_0 نیست (قضیهی کانتور)، آنگاه خواهیم دانست که اندازههای متفاوتی از بینهایت وجود دارند. این همان مفهومی است که عبارت 2aleph_0 را برایمان خاص میسازد.
بهعبارت دیگر، همیشه عددی بزرگتر از آنچه میپنداریم، وجود خواهد داشت. تعدادی نامحدود از اعداد اصلی بینهایت وجود دارند و بنابراین هرگز نمیتوان مفهومی را بهعنوان بزرگترین عدد اصلی» تعریف کرد.

الیور نیل ریاضیدانی از هاروارد میگوید:
اگر بخواهم عددی را بهعنوان عدد مورد علاقهی خود انتخاب کنم، این عدد مسلما، ثابت آپری یا (Zeta(3 میبود؛ چراکه هنوز رازورمزهای بسیاری درمورد آن وجود دارد.
در سال ۱۹۷۹، ریاضیدانی فرانسوی بانام راجر آپری، ثابت کرد که مقداری که بعدها بهعنوان ثابت آپری شناخته شد، عددی گنگ است. این عدد با ۱.۲۰۲۰۵۶۹ آغاز میشود و اعشار آن تا بینهایت ادامه پیدا میکند. این ثابت همچنین بهصورت مقدار تابع (Zeta(3 نیز شناخته میشود که در آن عدد ۳ بهعنوان ورودی تابع زتا (تابعی کشفشده از سوی ریمن) تعیین شده است.
یکی از بزرگترین مسائل دنیای ریاضی، فرضیهی ریمن است که به پیشبینی شرایطی میپردازد که در آن، تابع زتای ریمن برابر با صفر میشود؛ فرضیهای که اگر درست از آب درآید، این امکان را به ریاضیدانان خواهد داد تا دریابند اعداد اول چگونه توزیع شدهاند. دیوید هیلبرت، ریاضیدان معروف قرن بیستم درمورد فرضیهی ریمن میگوید:
اگر بعد از هزار سال هم از خواب بیدار میشدم، باز هم اولین پرسش من این بود که: آیا فرضیه ریمان ثابت شدهاست؟»
حال چهچیزی ثابت آپری را تااینحد برابمان جذاب کرده است؟ امروزه روشن شده است که ثابت آپری جایگاه ویژهای در علم فیزیک دارد، بهخصوص نقش آن در معادلات حاکم بر نیروی مغناطیسی الکترون و جهت تکانهی زاویهای آن.

اد لتزر، ریاضیدانی از دانشگاه تمپل در فیلادلفیا درمورد شگفتانگیزترین عدد شناختهشده، پاسخی تجربی ارائه کرده است:
من فکر میکنم این، پاسخی کسالتبار است؛ اما من باید عدد یک را بهعنوان عدد دلخواه خود برگزینم؛ چراکه ازسویی هم یک عدد است و ازسوی دیگر، دربارهی بسیاری از زمینههای انتزاعی، نقشهای متفاوتی ایفا میکند.
یک تنها عددی است که تمامی اعداد دیگر بدان بخشپذیر هستند. همچنین یک تنها عددی است که تنها بر یک عدد مثبت (یعنی خودش) بخشپذیر است و یک تنها عددی است که نه عددی اول محسوب میشود و نه مرکب.
در ریاضیات و مهندسی، اغلب اعداد بهصورت مقادیر میان صفر و یک بیان میشوند. عبارت صددرصد» تنها یک عبارت فانتزی برای گفتن عدد یک است. یک، عددی جامع و کامل است.
و البته در تمامی علوم بشری، یک بهعنوان واحدی بنیادین شناخته میشود. مثلا گفته میشود یک پروتون تنها باری بهاندازهی ۱+ دارد. در منطق دودویی، یک بهمعنای بله» است و همچنین یک بهعنوان عدد اتمی سبکترین عنصر دنیا شناخته شده است و نهایتا یک بهعنوان ابعاد یک خط مستقیم نیز تلقی میشود.

اتحاد اویلر که درواقع یک معادله است، بهمعنای واقعی کلمه، جواهری در ریاضیات بهحساب میآید. حداقل شاید بتوان گفت این نظری است که ریچارد فینمن، فیزیکدان معاصر درمورد این معادله دارد .این معادله همچنین از لحاظ زیبایی با غزلی از شکسپیر قیاس شده است.
در یک کلام میتوان اینگونه گفت که اتحاد اویلر، پل ارتباطی میان مهمترین ثابتهای ریاضی جهان است: عدد پی، لگاریتم طبیعی و عدد موهومی i. دولین میگوید:
[این معادله] توانسته سه ثابت مهم را با مفهوم عدد صفر و مفاهیم ریاضیات پایه به یکدیگر پیوند دهد:
e^{i*Pi} + 1 = 0

 وقتی اعداد را در کودکی یاد میگیریم، آنها را کاملا میپذیریم؛ اما داشتن توانایی تشخیص اینکه مثلا عدد چهار واقعا نشاندهندهی چیست، نیازمند سطح پیچیدهای از توانایی شناختی است. مطالعات نشان دادهاند نخستیها و پرندهها نیز میتوانند نمادها را با اعداد ارتباط دهند؛ اما این نخستینبار است که چنین قدرتی در هها نشان داده شده است.
وقتی اعداد را در کودکی یاد میگیریم، آنها را کاملا میپذیریم؛ اما داشتن توانایی تشخیص اینکه مثلا عدد چهار واقعا نشاندهندهی چیست، نیازمند سطح پیچیدهای از توانایی شناختی است. مطالعات نشان دادهاند نخستیها و پرندهها نیز میتوانند نمادها را با اعداد ارتباط دهند؛ اما این نخستینبار است که چنین قدرتی در هها نشان داده شده است.
محیط آزمایشی طراحیشده در این مطالعه کاملا ساده و متشکل از سیستم اصلاحشدهای بود که قبلا برای بررسی توانایی تشخیص نمادهای عددی در کبوتر استفاده شده بود. در ابتدا، زنبورها بهصورت انفرادی در مارپیچی Yمانند آموزش میدیدند تا بتوانند بهدرستی یک نماد را با یک عدد یا برعکس تطبیق دهند. سپس، این موضوع بررسی میشد که آیا آنها میتوانند از دانش گذشتهی خود برای تطابقدادن علامت بهکاررفته برای نشاندادن یک عدد با اشکال دیگر نیز استفاده کنند یا خیر؛ مانند همان حالتی که عدد دو میتواند نشاندهندهی دو موز یا دو درخت یا دو کلاه باشد.
گروه اول زنبورها آموزش دیده بودند یک نماد را با یک تعداد خاص از عناصر مرتبط کنند؛ درحالیکه گروه دوم آموزش دیده بودند برعکس این را انجام دهند و یک تعداد خاص را با یک نماد مطابقت دهند. پس از مرحلهی آموزش، زنبورها وارد فضای تصمیمگیری میشدند که در آن فضا، باید یک علامت و بنابراین اتاق مربوطبه نشانهای را انتخاب میکردند که قبلا دربارهاش آموزش دیده بودند؛ مثلا نماد N نشاندهندهی دو مورد و نماد T برعکس نشاندهندهی سه مورد بود. اگر آنها انتخاب درستی میکردند، پاداش آنها واردشدن به فضایی بود که در آن، شهدی شیرین وجود داشت و اگر در انتخاب خود اشتباه میکردند، وارد فضایی میشدند که مادهای بدمزه درانتظارشان بود.

 این موضوع نشان میدهد پردازش و درک عددی نمادها در مناطق مختلفی از مغز زنبورها اتفاق میافتد، همانند پردازشهای جداگانهای که در مغز انسان رخ میدهد. نتایج ما نشان میدهد توانایی زنبورهای عسل بهاندازهی توانایی برخی حیوانات برای یادگیری نمادها بهعنوان اعداد و انجام وظایف پیچیده نیست.
این موضوع نشان میدهد پردازش و درک عددی نمادها در مناطق مختلفی از مغز زنبورها اتفاق میافتد، همانند پردازشهای جداگانهای که در مغز انسان رخ میدهد. نتایج ما نشان میدهد توانایی زنبورهای عسل بهاندازهی توانایی برخی حیوانات برای یادگیری نمادها بهعنوان اعداد و انجام وظایف پیچیده نیست. انسانها بیش از ۸۶ میلیارد نورون در مغز خود دارند و زنبورها کمتر از یک میلیون. ما بیش از ۶۰۰ میلیون سال است که در مسیر تکامل ازهم جدا شدهایم؛ اما اگر زنبورها میتوانند چیزی به پیچیدگی زبان نمادین ساخت بشر را یاد بگیرند، این امر مسیرهای هیجانانگیز جدیدی درزمینهی ارتباط بین گونهها بازمیکند.
انسانها بیش از ۸۶ میلیارد نورون در مغز خود دارند و زنبورها کمتر از یک میلیون. ما بیش از ۶۰۰ میلیون سال است که در مسیر تکامل ازهم جدا شدهایم؛ اما اگر زنبورها میتوانند چیزی به پیچیدگی زبان نمادین ساخت بشر را یاد بگیرند، این امر مسیرهای هیجانانگیز جدیدی درزمینهی ارتباط بین گونهها بازمیکند.
گروهی از پژوهشگران حین انجام تحقیقاتی در زمینهی یادگیری ماشین، با سؤالاتی مواجه شدهاند که ارتباط تنگاتنگی با مسئلهای حلنشدنی در ریاضیات دارد. این مسئله به فرضیهی پیوستار» معروف است. در دههی ۱۹۳۰، کورت گودل، ریاضیدان اتریشی، اولینبار ادعا کرد این مسئله حلنشدنی است.
مسئلهای که این پژوهشگران با آن روبهرو بودند، مسئلهی یادگیری» نام دارد. این مسئله بررسی میکند آیا میتوان با استفاده از دادههای محدود، الگوریتمی برای حدسزدن الگوها یافت یا خیر. طبق مقالهای که ۷ژانویه (برابر با ۱۷دی) در مجلهی Nature Machine Intelligence منتشر شد، این مسئله صورت جدیدی از فرضیهی اثباتنشدهی پیوستار در ریاضیات است.
بهگفتهی امیر یهودیف، یکی از نویسندگان این مقاله، دستیابی به چنین مطلبی برای ما بسیار تعجبآور بود. البته، یافتن مسئلهای حلنشدنی در ریاضیات موضوع جدید و عجیبی نیست؛ اما تبدیلشدن مسئلهای ساده در یادگیری ماشین به چنین مسئلهی پیچیدهای در ریاضیات شگفتآور است.
بهعقیدهی جان توکر، متخصص علوم کامپیوتر، این مقاله نتیجهای بسیار ارزشمند است که مفاهیم پایهای برای هر دو شاخهی ریاضیات و یادگیری ماشین در پی دارد.
فرض پیوستار در ریاضیات، فرضیهای است که دربارهی اندازهی مجموعههای نامتناهی اظهارنظر میکند. طبق این فرضیه، هیچ مجموعهای وجود ندارد که اندازهی آن بین اندازهی مجموعهی اعداد صحیح و اندازهی مجموعهی اعداد حقیقی باشد.
دانشمندان یادگیری را اینگونه تعریف میکنند:
توانایی یک الگوریتم برای وسیعکردن دانش کسبشده بهوسیلهی خودش. این نوع الگوریتم معمولا به سؤالی مشخص جواب بله» یا خیر» میدهد. برای مثال، میتوان الگوریتمی طراحی کرد که پس از تغذیه با استفاده از تعدادی تصویر گربه، بتواند به این پرسش برای تصویری جدید که قبلا ندیده پاسخ دهد: آیا در تصویر گربهای وجود دارد؟
یهودیف و همکارانش هنگام کار روی مسئلهی یادگیری و مسئلهی فشردهسازی، به فرضیهی پیوستار برخوردند. هدف آنها این بود همهی ویژگیهای مهم یک مجموعه را در مجموعهای کوچکتر خلاصه کنند. این پژوهشگران در مسیر پاسخ به این پرسش به مسئلهای در نظریهی مجموعهها میرسیدند.
جورج کانتور، مبدع نظریهی مجموعهها، در دههی ۱۸۷۰ بیان کرد همهی مجموعههای نامتناهی باهم برابر نیستند. بهطور خاص، مجموعهی اعداد صحیح از مجموعهی اعداد حقیقی کوچکتر است؛ هرچند هر دوِ آنها مجموعههایی نامتناهی (دارای بیشمار عضو) هستند. کانتور همچنین حدس زد هیج مجموعهای وجود ندارد که اندازهی آن بین اندازهی مجموعهی اعداد صحیح و اعداد حقیقی باشد. او و بسیاری از ریاضیدانان و فلاسفهی پس از او، موفق نشدند این حدس را اثبات کنند.
درواقع، همهی تلاشهای آنها در این زمینه بیهوده بود؛ زیرا در سال ۱۹۴۰، گودل نشان داد با درنظرگرفتن اصول استاندارد، نمیتوان این فرضیه را رد یا اثبات کرد. در دههی ۱۹۶۰، کوهن، ریاضیدان آمریکایی، دیدگاههای گودل دراینباره را تکمیل کرد. تأیید یا تکذیب فرضیهی پیوستار، همانند تأیید یا تکذیب اصل توازی اقلیدسی در هندسه که ما را به هندسی اقلیدسی یا هذلولی یا ریمانی هدایت میکند، به ما تئوری سازگار جداگانهای در ریاضیات میدهد.
گودل و کوهن نشان دادند اگر فرضیهی پیوستار درست باشد، اصولی یکدست در ریاضیات پدید میآید و اگر نادرست باشد، اصولی کاملا متفاوت و جداگانه بهوجود میآید.

در مقالهی یهودیف و همکارانش، یادگیری بهعنوان نوعی توانایی تعریف میشود. با داشتن این توانایی، میتوان با مدلسازی مجموعههای کوچک دربارهی ویژگیهای مجموعههای بزرگتر حدسهایی زد. نکتهی مشترک مسئلهی یادگیری با فرضیهی پیوستار این است که بیشمار راه برای تعیین مجموعهی مدل وجود دارد؛ اما تعداد این راهها مشخص نیست. یهودیف میگوید:
اگر فرضیهی پیوستار درست باشد، جمعآوری نمونهای متناهی برای مدلسازی کافی است؛ اما اگر فرضیهی پیوستار درست نباشد، مجموعهی متناهی برای این کار کافی نیست.
بهعقیدهی یهودیف، اگر واقعا بخواهیم مسئلهی یادگیری را بفهمیم، درک ارتباط بین فشردهسازی و تعمیمدادن مدل به مجموعهی نامتناهی امر مهمی است.
دانشمندان تعدادی مسئلهی حلنشدنی دیگر مشابه آنچه گفته شد، در طول ادوار مختلف یافتهاند. برای نمونه، الن تیورینگ، مبدع نظریهی الگوریتمها، مسائلی طراحی کرد که هیچ رایانهای نمیتواند آنها را طی چند مرحلهی متناهی انجام دهد. باوجوداین، فرضیهی پیوستار مسئلهی حلنشدنی بسیار خاصی است که احتمال دارد ناشی از گونهای ناکاملی در زبان ریاضیات باشد. این فرضیه تأثیر مهمی در تئوری یادگیری ماشینی دارد؛ هرچند درعمل، احتمالا تأثیر خاصی نخواهد داشت.

اگر با مبحث همگرایی سریها آشنا باشید، احتمالاً از قبل میدانید که بسیاری از سریها مانند سری زیر به یک عدد همگرا میشوند.
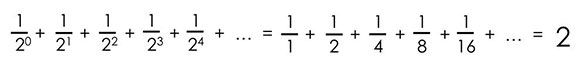
در مقابل، سریهایی مانند مثال زیر نیز وجود دارند که واگرا هستند یا به اصطلاح به بینهایت همگرا میشوند.
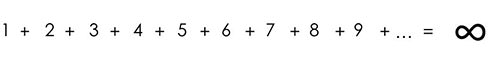
اما نظر شما دربارهی سری زیر چیست؟
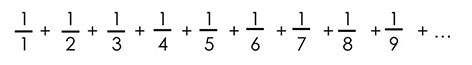
آیا این سری هم مانند مثال اول به یک عدد همگرا میشود یا مانند مثال دوم واگرا است؟
سری بالا که سری هارمونیک نام دارد بر خلاف باور بسیاری از افراد یک سری واگرا است. درست است که با بزرگ شدن مخرج کسر تا بینهایت، جملات به سمت صفر میل میکنند، اما سری هارمونیک با روندی بسیار بسیار آهسته به بینهایت میرود.
اثبات آن نیز به این صورت است:
بیایید سری هارمونیک را با یک سری کوچکتر از خودش مقایسه کنیم.
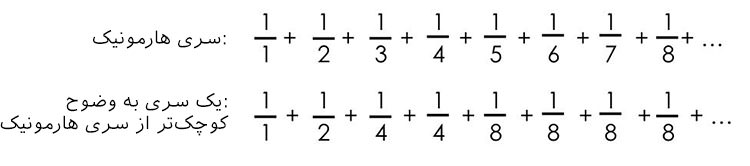
اگر دقت کنید در سری دوم، تمامی جملات کوچکتر یا مساوی با جملات سری هارمونیک است. (پس از آخرین جمله، ۸ جمله یک شانزدهم، و پس از آن ۱۶ جمله یک سی و دوم است و به همین ترتیب جملات ادامه خواهند داشت.)
حالا بیایید نگاه دقیقتری به سری دوم بیندازیم.
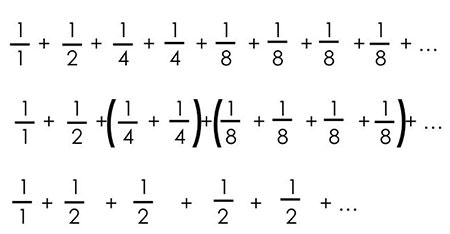
همانطور که مشخص است میتوان سری دوم را به صورت ۱ به اضافهی بینهایت جمله با مقدار یک دوم بازنویسی کرد. جمع این مقادیر به وضوح بینهایت میشود.
پس اگر
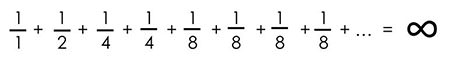
و
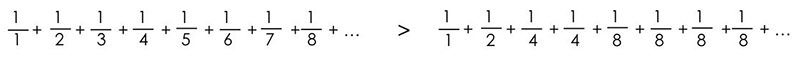
آنگاه

آیا احتمال اینکه شما نسبت به دوستانتان، از تعداد دوستان بیشتری برخوردار باشید بیشتر است؛ یا دوستانتان احتمالاً به صورت میانگین تعداد دوستان بیشتری از شما خواهند داشت؟ یا اینکه فکر میکنید وقتی صحبت از تصادفی» و میانگین» به میان میآید، دو احتمال مطرح شده در بالا با هم برابر است و نمیتوان از قبل دربارهی تعداد دوستان یک نفر نسبت به رفقایش اظهار نظر کرد؟
جواب مسئلهی بالا به این صورت بیان میشود:
تعداد دوستان اکثر افراد، از میانگین تعداد دوستان رفقایشان کمتر است!»
اما جملهی بالا به چه معنا است؟ عبارت فوق به زبان ساده یعنی اگر یک نفر را به صورت تصادفی انتخاب کنیم، به احتمال زیاد نسبت به دوستان خود از تعداد کمتری دوست برخوردار است.
این پدیده که مربوط به ریاضیات کاربردی است، با توجه به خواص ریاضی شبکههای اجتماعی» توجیه میشود.
در نگاه اول به نظر میرسد که وقتی یک نفر را به صورت تصادفی انتخاب کنیم، احتمال اینکه شخص مورد نظر از دوستان خود مشهورتر باشد (دوستان بیشتری داشته باشد) یا اینکه دوستانش از اون مشهورتر باشند (دوستان بیشتری داشته باشند) نباید با هم تفاوتی داشته باشد.
در مقالهای که در سال ۱۹۹۱ توسط اسکات فلد جامعه شناس منتشر شد، ۷۴ درصد افراد دوستان کمتری نسبت به میانگین تعداد دوستان رفقایشان داشتند. نکتهی اساسی در اینجا افراد مشهور» هستند.
بیایید یک مثال را با هم بررسی کنیم. شبکهی دوستی زیر را در نظر بگیرید:

در این شبکه هر نفر به صورت میانگین ۲.۸۵ دوست دارد، اما دوست هر نفر به صورت میانگین ۳.۳۹ دوست دارد. این مورد تنها یک مثال برای نشان دادن ممکن» بودن چنین حالتی است، اما از آن برای اثبات این اصل به صورت کلی نمیتوان استفاده کرد.
تا قبل از ظهور شبکههای اجتماعی آنلاین»، تحقیق دربارهی صحت این حقیقت کار دشواری بود، اما با آمدن فیسبوک، توییتر و اینستاگرام، به راحتی میتوان درستی پاسخ ارائه شده به این مسئله را بررسی کرد.
مسئلهی فوق به پارادوکس دوستی مشهور است و با استفاده از نامساوی کوشی-شوارتز میتوان آن را به راحتی اثبات کرد.
یک چهار ضلعی دلخواه رسم کنید. این چهارضلعی میتواند مقعر، محدب، نامنظم و به طور کلی به هر شکلی که دوست دارید باشد؛ تنها کافی است چهار ضلعی مورد نظر از چهار زاویه و خطوط راست تشکیل شده باشد.

نقطهی میانی هر ضلع را پیدا کرده و آنها را به یکدیگر متصل کنید.

همانطور که میبینید، نتیجه همواره یک متوازی الاضلاع است.
سه زندانی در سه سلول جدای از هم هستند و هر سه محکوم به اعدام شدهاند. قاضی به صورت تصادفی یکی از زندانیها را عفو میکند. نگهبان میداند که کدام زندانی مشمول عفو شده است، اما از گفتن نام او خودداری میکند.
زندانی A که خیلی دوست دارد بداند فردا قرار است اعدام شود یا خیر، از نگهبان میپرسد که به او بگوید کدام یک از دو زندانی B و C قرار است اعدام شود. سوال او از نگهبان به این صورت است:
که اگر B عفو شده است، نام C را به من بگو و اگر C عفو شده، نام B را به من بگو. اگر هم من عفو شدهام، سکهای بینداز و بین B و C نام یکی را به صورت تصادفی بگو.
نگهبان نام زندانی B را میگوید.
زندانی A خوشحال شده و با خود فکر میکند که شانس عفو شدن او از یک سوم به یک دوم افزایش یافته است، چرا که گزینههایی که ممکن است مورد عفو قرار بگیرند، تنها از بین A و C خواهند بود.
زندانی A در این باره به زندانی C خبر میدهد تا او را نیز خوشحال کند. زندانی C از زندانی A هم خوشحالتر میشود و به او میگوید:
شانس تو برای عفو شدن همچنان یک سوم است، در حالی که شانس من به دو سوم افزایش یافته است.
حق با کدام زندانی است؟
هر سه زندانی در ابتدا یک سوم شانس عفو داشتند. نگهبان نام B را بر زبان آورده است که با توجه به سوال زندانی، میتواند یکی از دو معنای زیر را داشته باشد:
این یعنی شانس اینکه A عفو شود نصف شانس عفو C است. B نیز هیچ شانسی برای عفو ندارد و محکوم به فنا است. با توجه به اینکه مجموع احتمال باید برابر ۱ شود، پس احتمال عفو A همان یک سوم و احتمال عفو C دو سوم است.
اگر تجزیه و تحلیل جملات بالا برایتان سخت است، در زیر پاسخ معما را به صورت تصویری با هم مرور خواهیم کرد. شکل زیر تمام حالات ممکن قبل از انداختن سکه را نشان میدهد:

از آنجایی که نگهبان نام B را گفته است، تنها با این حالات روبرو هستیم:

همانطور که در تصویر بالا میبینید شانس B برای عفو به 0 کاهش یافته و شانس C دو برابر شانس B است.
معماهایی که در این مجموعه مطرح شدند، همگی با استفاده از قوانین ابطال ناپذیر ریاضی قابل اثبات هستند. جدای از اثبات ریاضی، در مواردی که امکان شبیهسازی مسئله در دنیای واقعی وجود دارد، میتوان به روش آماری نشان داد که احتمالات به دست آمده (برای مثال در معمای مانتیهال، مسئلهی تاریخ تولد، جعبهی برتراند و معمای سه زندانی) در عمل هم برابر با همان مقداری است که پاسخ ریاضی مسئله پیشبینی کرده است.
پال اردیش ریاضیدان مجارستانی، یکی از کسانی است که بیشترین تعداد مقالات علمی منتشر شده در طول تاریخ به نام او ثبت شده است. حتی این ریاضیدان برجسته هم تنها پس از اینکه با چشمان خودش دید که در شبیهسازی کامپیوتری معمای مانتی هال، در صورت تعویض درب در دو سوم موارد برنده میشوید، حاضر به پذیرش پاسخ مسئله شد.
در بررسی آماری مسائل احتمال، یک مسئله هزاران یا میلیونها بار تکرار میشود تا ببینیم در عمل، شانس گزینههای مختلف چقدر است. مثلاً اگر هزاران بار سکه یا تاس بیندازیم، در عمل مشاهده خواهیم کرد که شانس هر گزینه به ترتیب برابر با یک دوم و یک ششم است. همانطور که در قسمت قبل اشاره کردیم، این متد به روش مونته کارلومشهور است. اردیش نیز که یک ریاضیدان بود و به صحت نتایج به دست آمده توسط روش مونته کارلو اطمینان داشت، وقتی پاسخ معمای مانتی هال با استفاده از این روش را دید، اشتباه خود را پذیرفت.
اما چرا عدهای باوجود انبوهی از اثباتهای ریاضی و شواهد تجربی، همچنان بسیاری از این معماها را حقههای ریاضی میدانند؟
یکی از دلایل فهم سخت مسائل احتمال، ادراکی (intuitive) نبودن چنین مسائلی است. درک مفاهیمی چون بینهایت» و بسیاری از مفاهیم احتمالات برای ذهن انسان بسیار دشوار است. از آنجایی که ما انسانها به صورت غریزی» درک درستی از این مفاهیم نداریم، باید با آنها از طریق آموزش» آشنا شویم.
استیون پینکر روانشناس در کتاب خود با نام The Blank Slate» اینگونه استدلال میکند که یکی از دلایل اصلی مشکل اکثر افراد با احتمالات، زبان تخصصی و گیج کنندهای است که برای بیان این قبیل مسائل از آن استفاده میشود. میتوانید اینجا به مطالعهی بیشتر در این زمینه بپردازید.
اما دستهی دیگری از افراد هستند که علاوه بر قبول نداشتن حقایق ریاضی، با اطمینان خاصی ادعای رد آنها را نیز دارند. این افراد نوابیغ» نامیده میشوند.
نوابیغ (با نوابغ اشتباه نشود) اصطلاحی است که عفت چهره گشا و دکتر عبادالله محمودیان، استاد ریاضیات دانشگاه صنعتی شریف و عضو انجمن ریاضی ایران، برای اشاره به کسانی که سعی در حل معماهای ناممکن یا رد اصول اثبات شده دارند، به کار بردهاند. نوابیغ به چند دسته تقسیم میشوند:

بینهایت عدد در دنیای ریاضی وجود دارد. در کنار آنها، بی نهایت روش برای ترکیب و دستکاری این اعداد فراهم است. ریاضیدانها اغلب، اعداد را بر روی محور اعداد نمایش میدهند و هر نقطه بر روی این محور، نمایانگر یک عدد است.
تقریبا، تمام اعدادی که با آنها سر و کار داریم جزیی از بنیادیترین اعداد موجود در ریاضی هستند. آنچه در ادامه به آن اشاره خواهیم داشت، هشت عددی هستند که مجموعهی کل اعداد را تشکیل میدهند و برای محاسبات کمی میتوانند مورد استفاده قرار بگیرند.
صفر نشان دهندهی عدم وجود است. ضمن این که صفر یک عنصر ضروری از سیستم اعداد به شمار میآید. صفر در واقع کمک میکند تا تفاوت نوشتاری اعداد یک رقمی با اعداد چند رقمی مشخص شود. به همین دلیل است که ما به راحتی فرق ۲ دلار با ۲۰ دلار را متوجه میشویم.
صفر به خودی خود عدد بسیار مهمی در ریاضی است. چرا که "هویت افزودنی" دارد و با هر عددی که جمع شود حاصل، خود آن عدد میشود. این ویژگی صفر، به آن نوعی مرکزیت در حساب و جبر بخشیده است. از این رو صفر دقیقا در وسط محور اعداد قرار میگیرد تا اعداد مثبت و منفی را از هم جدا کند و نقطهی شروعی برای ساخت سیستم اعداد در نظر گرفته شود.
در حالی که صفر هویت افزودنی دارد، عدد یک دارای هویت مضربی است. به این شکل که حاصل ضرب هر عدد در یک، خود آن عدد است. برای ادامهی محور اعداد نیاز به عدد یک داریم که باقی اعداد را با جمع یک به آن اضافه کنیم. در حالت خاص، میتوان اعداد طبیعی را مثال زد که از یک شروع میشود و به ترتیب ۲ و ۳ و ۴ تا بینهایت ادامه پیدا میکنند. اعداد طبیعی، اساسیترین اعداد ما هستند. به طوری که با استفاده از آنها اشیا و اشخاص را شمارش میکنیم. ضمن این که میتوانیم با آنها حساب و کتاب انجام دهیم. چنانچه یک عدد طبیعی را با یک عدد طبیعی دیگر جمع یا در آن ضرب کنیم، حاصل باز هم یک عدد طبیعی خواهد بود. البته در مورد تفریق و تقسیم، گاهی این حالت برقرار است.
همیشه تفریق دو عدد طبیعی برابر با یک عدد طبیعی نیست. از این رو اعداد طبیعی پاسخگوی تمام محاسبات نیستند و برای تفریق عبارتی مثل ۸-۳ جوابی ندارند. یکی از جنبههای فوقالعادهی دنیای ریاضی این است که هرگاه با محدودیتی روبرو شویم میتوانیم با گسترش سیستم اعداد، آن محدودیت را از بین ببریم. از این رو با افزودن عدد ۱- ، اعداد منفی شکل خواهند گرفت.
ضمن این که با حاصل ضرب ۱- در دامنهی اعداد مثبت، نسخهی منفی آنها تشکیل خواهد شد. علاوه بر این، اعداد منفی محدودیت در تفریق را هم بر طرف میکنند. به طوری حاصل ۸-۳ عدد ۵- میشود. بنابراین مجموعهای از اعداد مثبت، صفر و منفی خواهیم داشت که امکان تفریق تمام اعداد این مجموعه را فراهم میکنند. اعداد منفی در نشان دادن کم و کسری مفید هستند. برای مثال وقتی ۵۰۰ دلار به بانک بدهکار باشید، تراز بانکی شما ۵۰۰- دلار است. همچنین این اعداد در گزارش کمیتهای فیزیکی مانند دمای زیر صفر هم کاربرد دارند.
با وجود اعداد صحیح، باز هم مجموعهی اعداد مورد نیاز ناقص است. درست است که دیگر در جمع و تفریق محدودیتی مشاهده نمیشود اما در ضرب و تقسیم آزادی عمل نداریم. برای مثال نمیتوانیم حاصل دقیق ۵÷۸ را محاسبه کنیم. برای رویارویی با این حالت محور اعداد را به مقادیر ۱/۱۰ یا ۰.۱ تقسیم بندی میکنیم. به وسیلهی ۰.۱ و توانهای بالاتر آن مثل ۰.۰۱، ۰.۰۰۱، ۰.۰۰۰۱ وغیره میتوان کسر اعشاری حاصل را نمایش داد.
تقسیم دو عدد صحیح بر یکدیگر (به جز تقسیم بر صفر) به یک عدد ده دهی خاتمه پیدا میکند. برای مثال حاصل ۵÷۸ برابر با ۱.۶ است. یا حاصل ۳÷۱ برابر .۰.۳۳۳۳۳۳۳ است که رقم اعشاری ۳ تا بی نهایت ادامه خواهد داشت.
این نوع از اعداد که ارقام اعشاری آنها به مقداری معلوم خاتمه پیدا میکند یا الگوی مشخصی دارد، اعداد گویا هستند که نسبت دو عدد صحیح را نشان میدهند. در عملیاتی چون جمع، تفریق، ضرب و تقسیم اعداد گویا با یکدیگر، عدد حاصل هم یک عدد گویا است.
از طرفی اعداد گویا اجازه میدهند که مقادیر بین اعداد صحیح یا مقادیر کسری قابل بیان باشند. به همین خاطر ۴ نفر دوست میتوانند یک کیک را به چهار قسمت مساوی بین خود تقسیم کنند و سهم هر کدام ۱/۴، ۰.۲۵ یا ۲۵ درصد از کل کیک محاسبه شود. در واقع اعداد گویا کمک میکنند تا فضای بین عددهای صحیح در محور اعداد پر شود.
جذر دوم یک عدد، رقمی است که وقتی در خودش ضرب میشود، خود عدد را به عنوان پاسخ ارایه میدهد. برای مثال جذر دوم عدد ۹ برابر با ۳ است. چرا که: ۹=۳*۳. میتوان جذر هر عدد مثبت را در ریاضی پیدا کرد. البته در این میان تعداد کمی استثنا وجود دارد که جذر آن یک عدد گویا به دست نمیآید.
جذر عدد ۲ یکی از این استثناها است. جذر ۲ یک عدد گنگ است که در مقدار دسیمال آن هیچ الگوی مشخصی وجود ندارد. حاصل جذر ۲ رقمی به این شکل است: . ۱.۴۱۴۲۱۳۵۶۲۳۷ که ارقام بعد از اعشار، عجیب و غریب و تصادفی به نظر میرسند.
حتی گاهی جذر گویاترین اعداد، اعداد گنگ است. البته استثناهایی مانند ۹ وجود دارند که مربع کامل نامیده میشوند. ریشههای مربع در مبحث جبر اهمیت زیادی دارند و راه حل بسیاری از معادلات به حساب میآیند. برای مثال جذر عدد ۲ پاسخ معادلهی x2 = 2 است.
با قرار دادن اعداد گویا در کنار اعداد گنگ، محور اعداد ما کامل خواهد شد. به این صورت، به طیف گستردهی مجموعهی این اعداد، اعداد حقیقی گفته میشود و این اعداد اغلب در تمام شیوههای محاسباتی کاربرد دارند. +حالا که محور اعداد ما تکمیل شد، میتوانیم سراغ بررسی دیگر اعداد گنک برویم.

عدد π، معادل نسبت محیط دایره به قطر آن است که میتوان آن را مهمترین عدد در هندسه در نظر گرفت. عدد π در هر فرمولی که شامل سطح دایرهای یا کروی باشد حضور دارد. برای مثال مساحت دایره با شعاع r با رابطهی πr2 محاسبه میشود و این رابطه برای محاسبهی حجم کره با شعاع r معادل (4/3)πr3 لست.
ضمن این که عدد π یکی از اعداد برجسته در توابع مثلثاتی سینوس و کسینوس هم به حساب میآید. در اینجا عدد π نشان میدهد که به ازای هر واحد 2π، تابع دوباره تکرار میشود. توابع مثلثاتی با کمک عدد π، نشان دهندهی تناوب و تکرار هستند و در توصیف معادلاتی چون امواج صوتی به کار برده میشوند. عدد π مانند جذر ۲، گنگ بوده و بسط دسیمال آن نه پایان پیدا میکند و نه روند تکرار مشخصی دارد. چند رقم اول این عدد برای اکثر ما آشنا است: .۳.۱۴۱۵۹
ریاضیدانها با استفاده از کامپیوترهای خیلی بزرگ توانستند ۱۰ تریلیون رقم اول اعشار عدد π را پیدا کنند. هر چند که اغلب برای انجام محاسبات، تنها به چند رقم اول اول اکتفا میشود.
عدد اویلر، e اساس کار توابع نمایی است. توابع نمایی بیانگر فرآیندهایی هستند که در یک دورهی زمانی به یک مقدار چند برابر یا نصف میرسند. برای مثال فرض کنید که دو خرگوش نر و ماده دارید. پس از یک ماه ۴ خرگوش خواهید داشت. پس از دو ماه ۸ خرگوش و پس از سه ماه این تعداد به ۱۶ خرگوش خواهند رسید. به طور کلی تعداد خرگوشها پس از n ماه 2n+1 عدد است.
e در اینجا یک عدد گنگ است که معادل آن .۲.۷۱۸۲۸ میشود و مانند دیگر اعداد گنگ، ارقام پس از اعشار آن از هیچ روند مشخصی پیروی نمیکنند. ex یک تابع نمایی طبیعی است که پایه و اساس معادلات نمایی را تشکیل میدهد.

علت خاص بودن ex کمی پیچیده است. در حساب دیفرانسیل و انتگرال مشاهده کردهاید که مشتق ex معادل ex است. به این معنا که برای یک مقدار مشخص x مقدار ex را داریم و ارزش تابع در هر نقطه با نرخ آن در همان نقطه برابری میکند. همین ویژگی، ex را در میان توابع، منحصر به فرد ساخته است و باعث شده است تا کاربردهای مفیدی در ریاضیات از خود نشان دهد.
ex در اکثر فرآیندهای نمایی کاربرد دارد. یکی از رایجترین کاربردهای ex محاسبهی بهرهی مرکب است. به این ترتیب چنانچه سرمایهی اصلی P، نرخ سود سالانه r باشد ارزش سرمایه گذاری پس از گذشت t سال با این فرمول محاسبه میشود: A = P*ert
به موضوع جذر اعداد مثبت اشاره کردیم. اما باید دید در مورد جذر اعداد منفی چگونه میتوان عمل کرد. جذر اعداد منفی، در محدودهی اعداد حقیقی تعریف ندارد. همانطور که میدانیم ضرب دو عدد منفی یک عدد مثبت است. از این رو نمیتوان انتظار داشت که ریشه دوم یک عدد، رقمی منفی باشد. اما قبلا مشاهده کردیم که با گسترش سیستم اعداد میتوان محدودیتهای موجود را رفع کرد.
پس برای پیدا کردن ریشهی ۱- چه باید کرد؟
در اینجا یک واحد موهومی به نام i را تعریف میکنیم تا جمع، تفریق، ضرب و تقسیم گروه دیگری از اعداد را معنادار سازد. این نوع از اعداد، اعداد مختلط نام گرفتند. اعداد مختلط خواصی عجیب و کاربردی از خود نشان میدهند. از آنجا که میتوان اعداد حقیقی را بر روی یک محور افقی نشان دهیم، اعداد مختلط هم بر روی یک صفحه قابل نمایش هستند. از این رو محور عمودی میتواند بیان گر جزو مختلط یک عدد حقیقی باشد.
هندسهی اعداد مختلط نتایج شگفت انگیز و زیبایی به همراه دارند و کاربردهای آنها در الکتریسیته و مهندسی برق قابل مشاهده است.

خدای دریا، خدای طوفان، خدای حاصلخیزی، خدای جنگ و… هر کدام مدیریت بخشی از جهان را بر عهده داشتند. تاریخ نشان داده است که انسان اولیه چنین پدیدههایی را به خداها، شیاطین و سایر عوامل ناشناخته نسبت میداد. قصههای اساطیری پر از خدایان و الهههایی است که ظاهرا نقش مهمی در زندگی انسانهای تاریخ باستان داشتهاند. اما با پیشرفت روش علمی و پاسخ تدریجی به سؤال علم چیست»، به مرور جوابهای منطقی برای هر پدیدهای یافتیم و همچنان خواهیم یافت. طبیعت از دیدگاه اجداد انسانی ما دو چهرهی کاملا متفاوت داشت؛ حاصلخیزی و باران، طوفان و طغیان رودخانهها، صاعقه، خشکسالی و فوران خاکستر آتشفشانها.
انسانهای اولیه جهان را بهعنوان عرصهی جدال ارواح و خدایان یا واجد یک روح انسانی تصور میکردند که گاهی مهربان و شفیق و گاهی خشمگین و عصبانی میشد. اجداد انسانی ما با این تخیل میتوانستند رفتار متناقض طبیعت را از دیدگاه خود توجیه کنند. آنها برای مهار قهر طبیعت در پی چاره بودند و با به کارگیری عقل و استدلال و منطق و با آزمون و خطا؛ روشها و ابزارهایی طراحی میکردند که زندگی روی زمین را ایمنتر یا کمخطرتر میکرد؛ برای مثال ابداع چرخ؛ اهرم و سایر ابزارها کارها را سادهتر میکرد.
بشر با به کارگیری عقل و تجربه دریافت که میتواند با گذاشتن تنهی درخت در عرض یک رودخانه و عبور از آن به سوی دیگر رودخانه دسترسی پیدا کند. این راهحلها هم عموما در گذر زمان تصحیح میشدند و از دل آنها راهحلهای بهتر و کارامدتر خلق میشد. مثلاْ شاید نیاکان ما طی سالها آزمون و خطا شکل تنهی درخت را که بهعنوان پل روی رودخانه سوار شده بود، بهبود دادند و نقایص آن را رفع کردند. شاید به تجربه دریافتند که بهتر است دو سر چوب را محکم کنند یا حتی از چوبهای دیگری استفاده کنند. در حقیقت همهی این راهحلها و ابزارها پاسخی به این پرسش بودند که چگونه میتوان بهتر و آسودهتر زندگی کرد.
اما همهی پرسشهای بشر به همینجا ختم نمیشدند، یعنی پاسخ بسیاری از پرسشها با آزمون و خطا و تجربه مشخص نمیشد. انسان اولیه همواره در پی تفسیر جهان و همچنین در جستجوی یافتن دلیل وقوع پدیدهها و راهی برای مهار طبیعت بوده است. باران های سیلآسا، طلوع و غروب خورشید، خشکسالی و حاصلخیزی مزارع، مرگ و میر کودکان و شیوع بیماری از دیدگاه بشر نمیتوانست بدون دلیل باشد. اجداد انسانی ما پرسشهای فلسفی و اندیشهورزی نیز داشتهاند. آنها از خود میپرسیدند منشاء انسان از کجا است؟ هدف از زندگی چیست؟ پس از مرگ چه اتفاقی میافتد؟


ناتوانی علم در تولید منافع برای طبقهی فقیر در دهههای اخیر، ناشی از دو عاملی است که با هم در کار بودهاند: دانشمندان نظری از نیازهای روزمرهی بشری فارغ بودهاند و دانشمندهای کاربردی بیشتر به منافع زودرس چسبیدهاند. پیشرفت سریع علم در قرن نوزدهم، به بروز این ذهنیت منجر شد که علم بهتنهایی قادر به حل تمامی مشکلات انسانی است؛ درنتیجه در دهههای اولیهی قرن بیستم، بسیاری از دانشمندان و تمداران پیشبینی کردند که علم، تمامی مشکلات انسانی را حل خواهد کرد و بر خوشبختی بشر خواهد افزود.
علم بهتنهایی میتواند مشکلاتی مثل گرسنگی و فقر، فقدان بهداشت و بیسوادی، خرافات، رسوم و سنتهای سستکننده، اتلاف وسیع منابع و ست کشور بهوسیلهی مردمی فاقد آب و غذا را حل کند؛ چه کسی میتواند امروزه علم را نادیده بگیرد؟ در هر زمانی ما به علم نیازمند هستیم. برای کپلر، علم، وسیلهی بهدستآوردن منافع مادی برای انسانها یا ساخت یک فناوری برای بهتر کردن دنیای ناقص ما نیست؛ بلکه برعکس، علم وسیلهی اعتلای ذهن انسان است، وسیلهای برای رسیدن به آرامش در تفکر دربارهی کمال ابدی خلقت.
درحالیکه علم قدیم بهدنبال قرائت کتاب طبیعت بهعنوان آثار صنع الهی بود، گرایش غالب در عصر ما، توسعهی دانش به قصد افزودن قدرت مادی و اقتصادی است و اینکه طبیعت را بهعنوان کالایی تلقی کنند که باید از آن بهرهبرداری کرد. سواستفاده از علم و فناوری در قرن گذشته، خسارات بسیار زیادی برای محیطزیست و بشر بهبار آورد و این باعث ایجاد نیتی در میان دانشمندان عصر ما شد. ماکس بورن در نامهای که در سال ۱۹۵۴ به اینشتین نوشت، دربارهی سواستفادههای بهعمل آمده از علم گفت:
اگر تجربهی دانشجو یا دانشآموزی داشته باشید احتمالاً با یافتههای علمی بسیاری در طول تحصیل سروکار داشتهاید، اما آیا تا به حال از خود پرسیدهاید که خود علم چیست و آن روش علمی چیست که این یافتهها با آن روش بهدست میآیند؟ منظور ما از علم همان "Science" است و کاری با دانش بشری که شاید شامل فلسفه و ادبیات و غیره شود، نداریم. مطالعهی تاریخ علم به ما نشان میدهد که دیدگاه بشر چگونه طی ۲۶۰۰ سال ، از زمان تالس تا به امروز توسعه پیدا کرده است. نکتهی جالب توجه اینجا است که توسعهی هر نظریه، از دل نقد آن نظریه در میآید؛ برای مثال براساس نظریهی تالس، زمین مثل کشتی روی آب قرار داشته است.
انکسیمندر به این نظریه نقد جالبی کرد و پرسید اگر زمین مثل کشتی روی آب اقیانوس است پس آن اقیانوس روی چه چیزی قرار دارد؟ سپس نظریه را چنین اصلاح کرد: هیچ چیزی که زمین را نگاه دارد وجود ندارد، زمین به این دلیل در حالت س است که فاصله اش از همه چیز یکسان است. در فقدان فیزیک، کیهانشناسی و روش علمی در شناخت و برآورد ابعاد جهان، انسان اولیه تصور میکرد زمین در بین تارتاروس و اورانوس قرار دارد. طبق اسطورهها فاصلهی اورانوس تا زمین بهحدی بود که اگر یک سندان برنزی از سقف آسمان به زمین بیفتد 9 روز و شب طول می کشد و روز دهم سندان به زمین میرسد.

تارتاروس نیز به همین مقدار تا زمین فاصله داشت و از دید اسطورههای یونان باستان، زئوس، تایتانها یا غولهای سرکش را به درون آن پرتاب کرده بود. همهی این داستان ها و اساطیر، تلاشی در جهت تفسیر جهان بوده است و این تلاشها از لحاظ تاریخی، جد پدری فیزیک امروزی محسوب میشود. بعدها این نظریهها به تدریج با نقد روی نقد توسعه پیدا کرد؛ آریستارخوس، مدل بطلمیوسی و سرانجام مدل کپرنیک. در سایهی نقد علمی هر نظریه، نظریهی جدیدی خلق میشد که منسجمتر و دقیقتر با واقعیت جهان سازگارتر بود.
مفهوم نیوتنی نیرو بعدها با نظریهی اینشتین وارد فاز نسبیت شد.
مثلا قوانین کپلر سازوکار جهان را بهمراتب بهتر از مدلهای پیشین توضیح میداد؛ همانطور که مفهوم نیوتنی نیرو بعدها با نظریهی اینشتین وارد فاز نسبیت شد. درواقع نظریهی جایگزین با تصحیح و حذف یک خطا یا اشتباه روایتی بهبودیافته از نظریهی قبلی است. برخی از نظریههای علمی بهعنوان نظریههای انقلابی مطرح میشوند؛ نظریههایی که دیدگاه رایج عصر را از بن و ریشه به چالش میکشند. برای نمونه داروین نظریهی رایج زیست شناسی را بهصورت بنیادین برهم زد. یا اکتشاف الکترون توسط تامسون بعد از ۲۴۰۰ سال، ایدهی تقسیمناپذیری اتم را از بین برد. در عصر حاضر نیز ساختمان نظریههای جدید، روی استخوانهای نقد و شناسایی خطاهای نظریهها قبلی بنا شدهاند.
مدل اتمی تامسون در سال ۱۹۰۳، خیلی زود در سال ۱۹۱۱ با مدل سیارهای رادرفورد جایگزین شد. نظریهی رادرفورد بیان میداشت که الکترونها در مدارهای دایرهای شکل به دور هستهی اتم در گردش هستند. این نظریه هم، زمان زیادی دوام نیاورد و در سال ۱۹۱۳ توسط نی بور واژگون شد. بور در نقد مدل رادرفورد اینطور استدلال کرد که اگر ذرات، مانند سیارات منظومهی شمسی به دور خورشید در گردش باشند، باید طبق معادلات الکترومغناطیس ماکسول که هر ذرهی باردار متحرک در یک میدان الکترواستاتیک از خود بهصورت امواج الکترومغناطیس انرژی ساطع میکند، به روی هسته سقوط کند.
از آنجایی که چنین اتفاقی نمیافتد، به همین دلیل الگوی اتمی رادرفورد با یک ایراد ساختاری مواجه میشود. درست همانگونه که ایدهی تالس دربارهی زمین، با نقد انکسیمندر به چالش کشیده شد و در سایهی این نقد، نظریههایی بهتر و ساختار یافتهتر و منسجمتر مطرح شد. کپرنیک، داروین، نیوتن، فارادی و ماکسول، اینشتین، ماندل، کریک و واتسون، هایزنبرگ، شرودینگر و. هر کدام با بهرهگیری از روش علمی، با نقد نظریههای پیشین، با خلق نظریههای انقلابی علمی، دیدگاه ما در قبال ساختار جهان را به طرز اساسی تغییر دادند.
درباره این سایت